Homework 5

Psychology 2812B FW23

Weekly homework assignments are comprised of two components: a Lab Component that your TA will guide you through in the weekly lab session, and a Home Component that you are to complete on your own. You must hand in both components. Both will count towards your grade.

Submit homework on OWL by 5:00 pm London ON time on the date shown in the Class Schedule.

Submit your homework assignment as a single RMarkdown file, using your last name and the homework assignment as a filename in the following format: gribble_n.Rmd where n is the homework assignment number.

Here is the R Markdown template file for this assignment: lastname_5.Rmd.

Lab Component

1. UCI Wisconsin Breast Cancer Dataset

The UCI Wisconsin Breast Cancer Dataset is a dataset of 569 breast cancer patients. Each patient has 30 features, including the patient’s diagnosis (malignant or benign) and 29 features that describe the patient’s tumour. The dataset is available in the mclust package. Install and then load the package, and use the glimpse() function to see the structure of the dataset.

library(tidyverse)
library(mclust)

data(wdbc)
wdbc <- tibble(wdbc)

glimpse(wdbc)

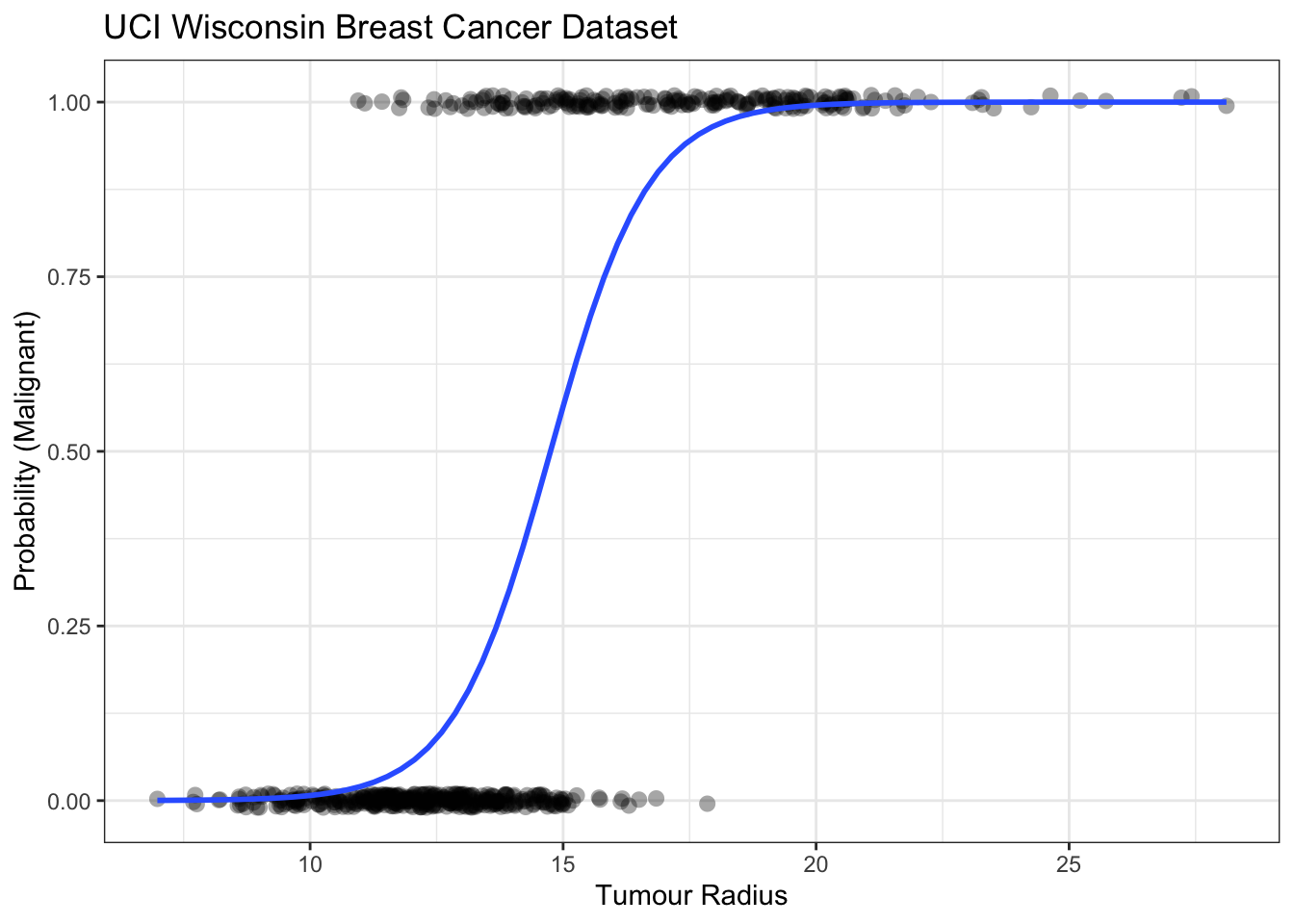
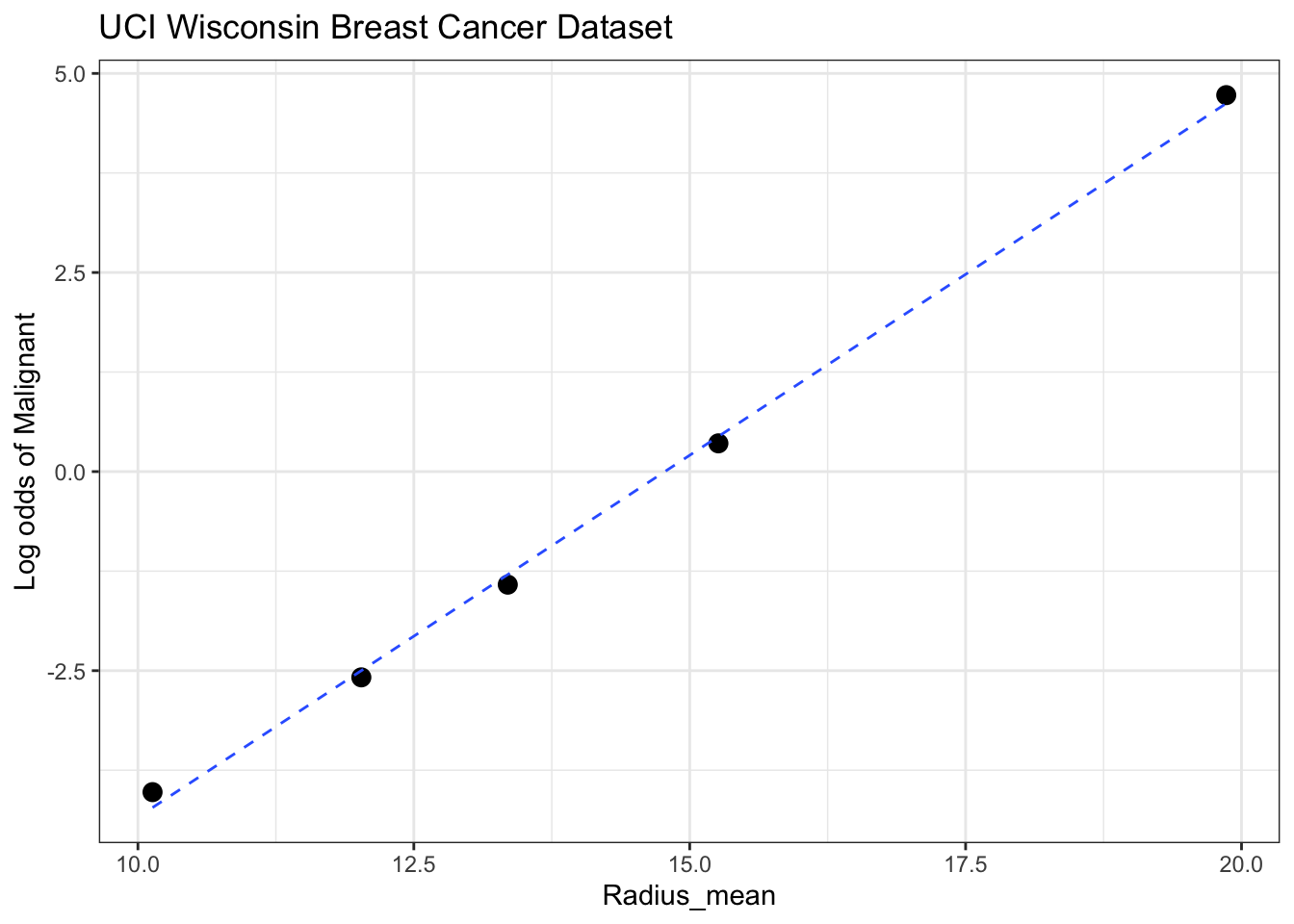
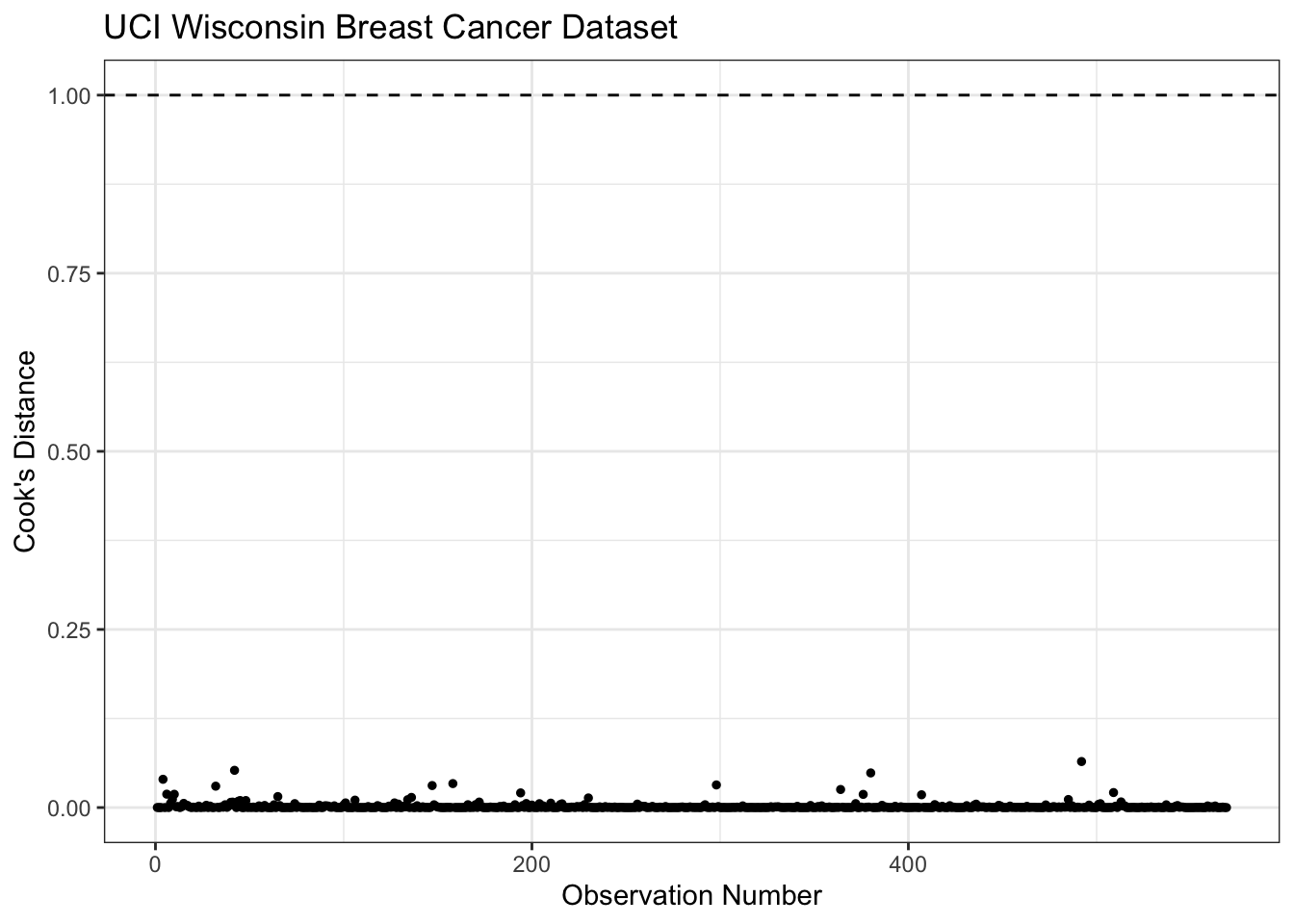
Rows: 569
Columns: 32
$ ID                  <int> 842302, 842517, 84300903, 84348301, 84358402, 8437…
$ Diagnosis           <fct> M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M,…
$ Radius_mean         <dbl> 17.990, 20.570, 19.690, 11.420, 20.290, 12.450, 18…
$ Texture_mean        <dbl> 10.38, 17.77, 21.25, 20.38, 14.34, 15.70, 19.98, 2…
$ Perimeter_mean      <dbl> 122.80, 132.90, 130.00, 77.58, 135.10, 82.57, 119.…
$ Area_mean           <dbl> 1001.0, 1326.0, 1203.0, 386.1, 1297.0, 477.1, 1040…
$ Smoothness_mean     <dbl> 0.11840, 0.08474, 0.10960, 0.14250, 0.10030, 0.127…
$ Compactness_mean    <dbl> 0.27760, 0.07864, 0.15990, 0.28390, 0.13280, 0.170…
$ Concavity_mean      <dbl> 0.30010, 0.08690, 0.19740, 0.24140, 0.19800, 0.157…
$ Nconcave_mean       <dbl> 0.14710, 0.07017, 0.12790, 0.10520, 0.10430, 0.080…
$ Symmetry_mean       <dbl> 0.2419, 0.1812, 0.2069, 0.2597, 0.1809, 0.2087, 0.…
$ Fractaldim_mean     <dbl> 0.07871, 0.05667, 0.05999, 0.09744, 0.05883, 0.076…
$ Radius_se           <dbl> 1.0950, 0.5435, 0.7456, 0.4956, 0.7572, 0.3345, 0.…
$ Texture_se          <dbl> 0.9053, 0.7339, 0.7869, 1.1560, 0.7813, 0.8902, 0.…
$ Perimeter_se        <dbl> 8.589, 3.398, 4.585, 3.445, 5.438, 2.217, 3.180, 3…
$ Area_se             <dbl> 153.40, 74.08, 94.03, 27.23, 94.44, 27.19, 53.91, …
$ Smoothness_se       <dbl> 0.006399, 0.005225, 0.006150, 0.009110, 0.011490, …
$ Compactness_se      <dbl> 0.049040, 0.013080, 0.040060, 0.074580, 0.024610, …
$ Concavity_se        <dbl> 0.05373, 0.01860, 0.03832, 0.05661, 0.05688, 0.036…
$ Nconcave_se         <dbl> 0.015870, 0.013400, 0.020580, 0.018670, 0.018850, …
$ Symmetry_se         <dbl> 0.03003, 0.01389, 0.02250, 0.05963, 0.01756, 0.021…
$ Fractaldim_se       <dbl> 0.006193, 0.003532, 0.004571, 0.009208, 0.005115, …
$ Radius_extreme      <dbl> 25.38, 24.99, 23.57, 14.91, 22.54, 15.47, 22.88, 1…
$ Texture_extreme     <dbl> 17.33, 23.41, 25.53, 26.50, 16.67, 23.75, 27.66, 2…
$ Perimeter_extreme   <dbl> 184.60, 158.80, 152.50, 98.87, 152.20, 103.40, 153…
$ Area_extreme        <dbl> 2019.0, 1956.0, 1709.0, 567.7, 1575.0, 741.6, 1606…
$ Smoothness_extreme  <dbl> 0.1622, 0.1238, 0.1444, 0.2098, 0.1374, 0.1791, 0.…
$ Compactness_extreme <dbl> 0.6656, 0.1866, 0.4245, 0.8663, 0.2050, 0.5249, 0.…
$ Concavity_extreme   <dbl> 0.71190, 0.24160, 0.45040, 0.68690, 0.40000, 0.535…
$ Nconcave_extreme    <dbl> 0.26540, 0.18600, 0.24300, 0.25750, 0.16250, 0.174…
$ Symmetry_extreme    <dbl> 0.4601, 0.2750, 0.3613, 0.6638, 0.2364, 0.3985, 0.…
$ Fractaldim_extreme  <dbl> 0.11890, 0.08902, 0.08758, 0.17300, 0.07678, 0.124…

2. Predicting cancer diagnosis using tumour radius: plot

We are interested in using the radius of the tumour (the Radius_mean variable) to predict whether the tumour is malignant or benign (the Diagnosis variable). Create a scatterplot with the radius on the horizontal axis and the diagnosis on the vertical axis. Use the geom_jitter() function to add a little random vertical jitter to the data points to aid in visualization (only vertical jitter, no horizontal jitter). Use the geom_smooth() function to add a logistic regression line to the plot. Use the labs() function to add a title, and to label the vertical axis as “Probability (Malignant)” and the horizontal axis as “Tumour Radius”. I also like to set size=2, stroke=0, alpha=0.5, fill="black" in the geom_jitter() function to make the points look a little nicer.

3. Predicting cancer diagnosis using tumour radius: model

Use the glm() function with option family="binomial" to fit a logistic regression model to the data in which you use Radius_mean to predict Diagnosis. Use the summary() function to see the results of the model. Don’t worry yet about testing the assumptions of logistic regression, you will do that later in the homework.


Call:
glm(formula = Diagnosis ~ Radius_mean, family = "binomial", data = wdbc)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -15.24587    1.32463  -11.51   <2e-16 ***
Radius_mean   1.03359    0.09311   11.10   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 751.44  on 568  degrees of freedom
Residual deviance: 330.01  on 567  degrees of freedom
AIC: 334.01

Number of Fisher Scoring iterations: 6

4. Predicting cancer diagnosis using tumour radius: predict

Use the predict() function to predict the probability that a tumour with radius 17 is malignant.

The probability that a tumour of radius 17 is malignant is 91 %

5. Predicting 50% chance of a malignant tumour

According to the model, what tumour radius is associated with a 50% chance of malignancy? Give your answer to 3 decimal places.

To solve this, remember the equations for the logistic regression model:

\log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 (\mathrm{Radius\_mean})

A tumour radius of 14.750 is associated with a 50 % chance of a malignant tumour.

6. Test the linearity of log odds assumption

6.1. Plot the log odds of the outcome against the predictor variable

One of the assumptions of logistic regression is that the predictor variable(s) is/are linearly related to the log odds of the outcome (the binary dependent variable).

To test this assumption, we can plot the log odds of the outcome against the predictor variable. If the relationship is linear, then the points should fall along a straight line. If the relationship is not linear, then the points will not fall along a straight line. Since the dependent variable is binary however, we cannot compute the log odds of each individual data point. Instead, we can bin the data into groups along the predictor variable, and then compute the mean log odds of the outcome for each group.

Create a new tibble containing the binned data, call it wdbc_binned. Use the cut() function to bin the data into 5 groups based on the Radius_mean variable, and define the breaks using the quantile() function so that there are approximately equal n within each of the 5 groups. Use the group_by() and summarize() functions to compute the mean log odds of the outcome for each group.

# A tibble: 5 × 5
  Radius_bin  bin_n bin_Radius bin_prob bin_log_odds
  <fct>       <int>      <dbl>    <dbl>        <dbl>
1 [6.98,11.4]   114       10.1   0.0175       -4.03 
2 (11.4,12.7]   114       12.0   0.0702       -2.58 
3 (12.7,14.1]   113       13.4   0.195        -1.42 
4 (14.1,17.1]   114       15.3   0.588         0.355
5 (17.1,28.1]   114       19.9   0.991         4.73

Now plot the mean log odds of the outcome (on the vertical axis) against the mean of the predictor variable for each group (on the horizontal axis). Use the geom_point() function to add the points to the plot, and use the geom_smooth() function to add a linear regression line to the plot. Use the labs() function to add a title, and to label the vertical axis as “Mean Log Odds of Malignancy” and the horizontal axis as “Mean Tumour Radius”.

What does the plot tell you about the assumption of linearity of log odds?

6.2. Statistical test of the linearity of log odds assumption

Perform a Box-Tidwell test of the linearity of log odds assumption by testing for an interaction between Radius_mean and log(Radius_mean). Use the glm() function with option family="binomial" to fit a logistic regression model to the data in which you use Radius_mean and log(Radius_mean) to predict Diagnosis. Use the summary() function to see the results of the model.


Call:
glm(formula = Diagnosis ~ Radius_mean + Radius_mean:log(Radius_mean), 
    family = binomial, data = wdbc)

Coefficients:
                             Estimate Std. Error z value Pr(>|z|)
(Intercept)                   -1.5023    14.4884  -0.104    0.917
Radius_mean                   -2.5398     3.7910  -0.670    0.503
Radius_mean:log(Radius_mean)   0.9799     1.0433   0.939    0.348

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 751.44  on 568  degrees of freedom
Residual deviance: 329.14  on 566  degrees of freedom
AIC: 335.14

Number of Fisher Scoring iterations: 7

What do the results of this model tell you about the assumption of linearity of log odds?

7. Test for outliers

Compute Cook’s distance for each observation in the dataset. Use the cooks.distance() function to compute Cook’s distance for each predicted probability in the dataset. Use the plot() function to plot Cook’s distance against the observation number. Use the geom_hline() function to add a horizontal line at Cook’s distance = 1.

What does the plot tell you about the presence of outliers in the dataset?

Home Component

8. Add more predictors to the model

You are interested in using more predictors than just tumour radius to predict malignancy.

Define a new tibble containing Diagnosis and only the following 5 predictor variables:

Radius_mean
Texture_mean
Smoothness_mean
Concavity_mean
Symmetry_mean

Fit a new model that includes these 5 predictor variables and show the model output using summary():

9. Test for collinearity

9.1. Plot the correlations between the predictors

Produce a plot using ggpairs() from the GGally package to visualize the correlation between the predictor variables.

What does the plot and the correlation coefficients tell you about the presence of collinearity in the dataset?

9.2 Test for collinearity using the variance inflation factor (VIF)

Use the vif() function from the car package to compute the variance inflation factor (VIF) for each predictor variable in the model. Use the summary() function to see the results of the VIF test.

What do the results of the VIF test tell you about the presence of collinearity in the dataset?

10. Model selection

Perform a stepwise procedure using step() to determine the best set of predictor variables for the model and interpret the output. Use the direction="both" option to perform a stepwise procedure that both adds and removes variables from the model. Describe and interpret the output of the stepwise procedure.

11. New model vs old model

11.1. Which model does a better job?

Which model does a better job of predicting malignancy in the training data, the model you fit in Question 3 above, or the model you fit in Question 10? Refer to a specific quantity or measure in your answer.

11.2. Predicting the probability of malignancy

In Question 4 above you used the model you fit in Question 3 to predict the probability that a tumour with radius 17 is malignant. Use the model you fit in Question 10 to predict the probability that a tumour with radius 17 is malignant. For the values of the other predictor variables in the model in Question 10, use the mean values in the dataset as your predictor values. How do the two predictions compare?