Repeated Measures ANOVA

Week 11

Final Exam

I will post some sample questions on the course website in the next week or so
review the lecture slides
review the readings
review the homeworks
focus on concepts first not the tiniest details

Repeated Measures Experiments

sometimes also called “within-subjects” or “within-participants”
the same participant is measured on the same dependent variable multiple times (more than 2)
(if only 2 measurements just use a paired samples t-test)

Repeated Measures Experiments

e.g. the same participant is measured on their mood (1) before and (2) after a treatment and then (3) again after a week
effects of placebo vs treatment A vs treatment B on blood pressure can be studied in the same participants, each participant can serve as their own control
behaviour of subjects can be studied over multiple time points

Advantages of Repeated Measures Designs

sometimes participants can serve as their own control
- (no need for a separate control group)
variance between levels of a factor is reduced
- no longer due to effect + inter-subject variability
- it’s the same subjects!
variance across levels of the factor is only due to the effect of the factor

Advantages of Repeated Measures Designs

more information is obtained from each participant than in a between-subjects design
within-subjects design: each subject contributes a scores
- (a = number of levels of the repeated-measures factor)
between-subjects design: each subject contributes only 1 score
the number of subjects required to reach a given level of statistical power is often much lower in a within-subjects design than in a between-subjects design

Advantages of Repeated Measures Designs

same subject measured in each level of the factor
variability in individual differences between subjects is removed from the ANOVA error term
ANOVA error term (denominator of the F ratio) is reduced
statistical power to detect an effect of the factor is increased

Example dataset

Code

library(tidyverse)
rmdata <- read_csv(url("https://www.gribblelab.org/2812/data/rmdata.csv"),
                   col_types="fnnn")
rmdata

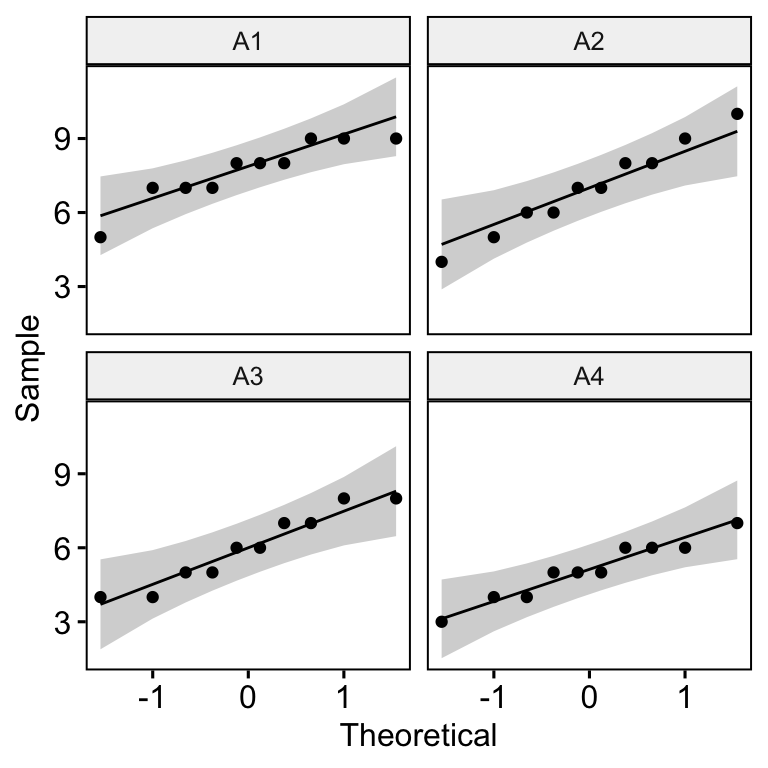
# A tibble: 10 × 5
   Subject    A1    A2    A3    A4
   <fct>   <dbl> <dbl> <dbl> <dbl>
 1 1           8    10     7     5
 2 2           9     9     8     6
 3 3           7     5     8     4
 4 4           9     6     5     7
 5 5           8     7     7     6
 6 6           5     4     4     3
 7 7           7     6     5     4
 8 8           8     8     6     6
 9 9           9     8     6     5
10 10          7     7     4     5

as an exercise let’s treat this dataset as a between-subjects design

Code

# convert from wide to long format
rmdata_long <- gather(rmdata, FactorA, DV, A1:A4, factor_key=TRUE)
# compute a between-subjects ANOVA
aov.bet <- aov(DV ~ FactorA, data=rmdata_long)
summary(aov.bet)

            Df Sum Sq Mean Sq F value  Pr(>F)   
FactorA      3   38.9  12.967   6.062 0.00189 **
Residuals   36   77.0   2.139                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

what we’re missing out on is the fact that some of the total variance in the data is due to differences between the subjects
what if we were to include a second factor called Subject that coded for the subject number?

Code

aov.bet2 <- aov(DV ~ FactorA + Subject, data=rmdata_long)
summary(aov.bet2)

            Df Sum Sq Mean Sq F value   Pr(>F)    
FactorA      3   38.9  12.967  12.241 3.06e-05 ***
Subject      9   48.4   5.378   5.077 0.000471 ***
Residuals   27   28.6   1.059                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

notice how the Sum Sq for Residuals is much smaller now
Mean Sq for Residuals (the “error term” for the ANOVA) is also much smaller
So our F value is much larger for Factor A

including `Subjects` reduces the ANOVA error term

48.4 + 28.6 = 77.0

including `Subjects` reduces the ANOVA error term

77.0 / 36 = 2.139
28.6 / 27 = 1.059

including `Subjects` increases `F`

12.967 / 2.139 = 6.062
12.967 / 1.059 = 12.241
a more statistically powerful test of the effect of Factor A
more likely to detect a true difference

Repeated Measures ANOVA

our little experiment including Subjects as a factor:

            Df Sum Sq Mean Sq F value   Pr(>F)    
FactorA      3   38.9  12.967  12.241 3.06e-05 ***
Subject      9   48.4   5.378   5.077 0.000471 ***
Residuals   27   28.6   1.059                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

this is in fact what repeated measures ANOVA does, essentially
it accounts for the differences in the DV across subjects,
and removes that variability from the error term

Repeated Measures ANOVA in R

the right way to do it (which becomes more important with multiple factors and more complex designs):

aov.rm <- aov(DV ~ FactorA + Error(Subject/FactorA), data=rmdata_long)
summary(aov.rm)


Error: Subject
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals  9   48.4   5.378               

Error: Subject:FactorA
          Df Sum Sq Mean Sq F value   Pr(>F)    
FactorA    3   38.9  12.967   12.24 3.06e-05 ***
Residuals 27   28.6   1.059                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Repeated Measures ANOVA in R

aov.rm <- aov(DV ~ FactorA + Error(Subject/FactorA), data=rmdata_long)
summary(aov.rm)


Error: Subject
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals  9   48.4   5.378               

Error: Subject:FactorA
          Df Sum Sq Mean Sq F value   Pr(>F)    
FactorA    3   38.9  12.967   12.24 3.06e-05 ***
Residuals 27   28.6   1.059                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Error(Subject/FactorA) is the way to tell the aov() function that FactorA is a within-subjects factor

Linear Models for Repeated Measures ANOVA

H_{1}: Y_{ij} = \mu + \alpha_{j} + \pi_{i} + \varepsilon_{ij}
H_{0}: Y_{ij} = \mu + \pi_{i} + \varepsilon_{ij}

Y_{ij} is the value of the DV for the ith subject at the jth level of the repeated measures factor
\mu is the grand mean of the entire dataset across all subjects and all levels of the repeated measures factor
\alpha_{j} is the effect of the jth level of the repeated measures factor
\pi_{i} is the effect of the ith subject
\varepsilon_{ij} is the unexplained varability in the ith subject at the jth level of the repeated measures factor

Linear Models for Repeated Measures ANOVA

H_{1}: Y_{ij} = \mu + \alpha_{j} + \pi_{i} + \varepsilon_{ij}
H_{0}: Y_{ij} = \mu + \pi_{i} + \varepsilon_{ij}

full model (H_{1}) includes the effect of the factor (\alpha_{j}) AND the effect of subjects (\pi_{i})
restricted model (H_{0}) only includes effect of subjects (effect of factor is zero)
null hypothesis H_{0} is that the factor \alpha_{j} has no effect on the DV; the only things that affect the DV are inter-subject differences \pi_{i} and random variability \varepsilon_{ij}

Assumptions of Repeated Measures ANOVA

random sampling from the population
independence of subjects
normality ^{*}
no extreme outliers ^{*}
homogeneity of treatment-difference variances ^{*}
- also called “sphericity”
- the variances of the differences between all pairwise combinations of groups are equal

Normality

some say it’s better to perform tests on each level of the RM factor

library(rstatix) # for shapiro_test()
rmdata_long %>%
    group_by(FactorA) %>%
    shapiro_test(DV)

# A tibble: 4 × 4
  FactorA variable statistic     p
  <fct>   <chr>        <dbl> <dbl>
1 A1      DV           0.871 0.102
2 A2      DV           0.984 0.982
3 A3      DV           0.918 0.341
4 A4      DV           0.952 0.691

library(ggpubr) # for ggqqplot()
ggqqplot(rmdata_long, "DV", facet.by="FactorA")

Extreme Outliers

we can use the identify_outliers() function from the rstatix package

library(rstatix) # for identify_outliers()
rmdata_long %>%
    group_by(FactorA) %>%
    identify_outliers(DV)

[1] FactorA    Subject    DV         is.outlier is.extreme
<0 rows> (or 0-length row.names)

0 rows = empty list so no outliers

Sphericity

homogeneity of treatment-difference variances
the variances of the differences between all pairwise combinations of groups are equal
Mauchly’s Test is the most common test for sphericity

Sphericity

if we use the ezANOVA() function from the ez package to perform our repeated measures ANOVA instead of the aov() function, we will automatically get:
- results of Mauchly’s test of sphericity
- Greenhouse-Geisser corrected F value and p value

Greenhouse-Geisser Correction

estimates epsilon (a metric of sphericity)
if sphericity is violated, epsilon is < 1.0
denominator df for the F-ratio is corrected (lowered) by multiplying with epsilon
F-ratio is recomputed using corrected df
some prefer the “Huynh–Feldt correction” which is slightly less conservative when sphericity is violated only slightly
ezANOVA() function shows both GG and HF corrected F and p values

Repeated Measures ANOVA in R using `ezANOVA()`

Code

library(ez)
rm.anova <- ezANOVA(data=rmdata_long, dv=DV, wid=Subject, within=FactorA)
rm.anova

$ANOVA
   Effect DFn DFd        F            p p<.05       ges
2 FactorA   3  27 12.24126 3.059801e-05     * 0.3356342

$`Mauchly's Test for Sphericity`
   Effect         W         p p<.05
2 FactorA 0.3461323 0.1488387      

$`Sphericity Corrections`
   Effect       GGe        p[GG] p[GG]<.05       HFe        p[HF] p[HF]<.05
2 FactorA 0.7426009 0.0002387789         * 0.9981017 3.106252e-05         *

ezANOVA() is a wrapper around aov() that makes it easier to do repeated measures (and mixed repeated-between) ANOVA
it computes Mauchly’s test of sphericity
and shows both GG and HF corrected F and p values

Repeated Measures ANOVA in R using `ezANOVA()`

Code

library(ez)
rm.anova <- ezANOVA(data=rmdata_long, dv=DV, wid=Subject, within=FactorA)
rm.anova

$ANOVA
   Effect DFn DFd        F            p p<.05       ges
2 FactorA   3  27 12.24126 3.059801e-05     * 0.3356342

$`Mauchly's Test for Sphericity`
   Effect         W         p p<.05
2 FactorA 0.3461323 0.1488387      

$`Sphericity Corrections`
   Effect       GGe        p[GG] p[GG]<.05       HFe        p[HF] p[HF]<.05
2 FactorA 0.7426009 0.0002387789         * 0.9981017 3.106252e-05         *

Some say one should always use the (GG or HF) corrected F and p values, because sphericity is never perfect (never exactly 1.0)
the corrections are graded—the less/more sphericity is violated, the more the correction
so the corrected F and p values are always more ‘correct’ than the uncorrected ones

Post-hoc tests

just like before with between-subjects ANOVA we can use emmeans() and pairs()

library(emmeans) # for emmeans() and pairs()
rm.anova <- aov(DV ~ FactorA + Error(Subject/FactorA), data=rmdata_long)
mm <- emmeans(rm.anova, specs = ~ FactorA)
pairs(mm, adjust = "holm")

 contrast estimate   SE df t.ratio p.value
 A1 - A2       0.7 0.46 27   1.521  0.1399
 A1 - A3       1.7 0.46 27   3.693  0.0040
 A1 - A4       2.6 0.46 27   5.649  <.0001
 A2 - A3       1.0 0.46 27   2.173  0.1163
 A2 - A4       1.9 0.46 27   4.128  0.0016
 A3 - A4       0.9 0.46 27   1.955  0.1219

P value adjustment: holm method for 6 tests

Disadvantages of Repeated Measures ANOVA

order effects
e.g. a neuroscientist wants to compare the effects of placebo vs drug A vs drug B on aggressiveness in monkeys
every pair of monkeys will be observed three times, once for each condition
how should we design the study?
one possibility: placebo day 1 then drug A day 2 then drug B day 3
bad idea: confounds potential drug effects with effect of time
maybe monkeys become less aggressive over time

Counterbalancing

one solution is to counterbalance the order of the conditions
some get [placebo day 1] -> [drug A day 2] -> [drug B day 3]
others get [placebo day 1] -> [drug B day 2] -> [drug A day 3]
we can do statistical tests to see if the order of the conditions matters
- e.g. by coding the order of the conditions as a between-subjects factor in the ANOVA

Latin Square Designs

but what if we have multiple levels of the within-subjects factor, e.g. A,B,C,D
many possible counterbalancing schemes (24 of them for 4 levels!)
not feasible to repeat our experiment with all of them
a Latin Square design is a way to counterbalance the order of the conditions in a principled way
every condition is presented exactly once in each row and column

Latin Square Designs

Differential Carryover Effects

a nasty problem with repeated measures designs
placebo -> drug A -> drug B
what if the drug A has a carryover effect that influences the DV in the drug B condition?
and
what if that is different than the carryover effect of drug B onto the DV in the drug A condition?
counterbalancing or Latin Squares will not help us here

Differential Carryover Effects

we could introduce a long “washout” period after one drug to let enough time elapse to eliminate the carryover effect
can’t always be done, some carryover effects are permanent
- (e.g. lesions, or some drugs, or learning & memory experiments)
some scientific questions are better suited to between-subjects designs

Other ANOVA designs

Mixed ANOVA: combination of between- and within-subjects factors
sometimes called “Split-Plot ANOVA”
e.g. factor A is “time” and has three levels, (day 1, day 2, day 3)
factor B is “drug” and has two levels (placebo, drug A)
DV is “aggressiveness” of a monkey
each monkey is randomly assigned to either placebo or drug A
each monkey is observed three times, once for each level of time
this is a mixed ANOVA design
- “time” is a within-subjects factor
- “drug” is a between-subjects factor

Other ANOVA designs

ANCOVA: Analysis of Covariance
ANOVA + a continuous variable as a “covariate”
often used to “control for” a nuisance variable that is correlated with the DV
e.g. we want to know if drug A has an effect on aggressiveness
maybe aggressiveness is known to vary with monkey size (weight)
we could add monkey weight as a covariate to the model
allows us to test the effect of the drug on aggressiveness after we have removed any differences in aggressiveness than can be accounted for by differences in monkey weight

Other ANOVA designs

MANOVA: Multivariate Analysis of Variance
ANOVA with multiple DVs
allows us to test for effects of one or more factors across multiple DVs at the same time, in a principled way that takes into account the multiple comparisons problem
also accounts for correlation between the different DVs

Other ANOVA designs

MANCOVA: Multivariate Analysis of Covariance
plus any other combo you can think of!
you can have any combination of within-subjects factors, between-subjects factors, covariates, multiple DVs, etc.
they are all just linear models with different combinations of predictors
- predictors can be continuous (e.g. a covariate)
- predictors can be categorical (e.g. a between-subjects or within-subjects factor)
- interactions between predictors are also in the model

Linear Mixed Effects Models

a generalization of ANOVA that allows us to model more complex designs
handles unbalanced designs and missing data much better than traditional ANOVA
can be used to model repeated measures designs
nested designs (e.g. children within classrooms within schools within school districts)

Go Forth And Do Science!

we have focused on concepts and main principles
we have not covered every tiny detail
all the complex approaches/models you will learn about next are just extensions of the basic concepts we have covered here
remember often there are different approaches
try to understand the tradeoffs, and choose for yourself
Data is currency in science
Good data comes from good experimental designs
Have fun!

Repeated Measures ANOVA

Final Exam

Repeated Measures Experiments

Repeated Measures Experiments

Advantages of Repeated Measures Designs

Advantages of Repeated Measures Designs

Advantages of Repeated Measures Designs

Example dataset

including Subjects reduces the ANOVA error term

including Subjects reduces the ANOVA error term

including Subjects increases F

Repeated Measures ANOVA

Repeated Measures ANOVA in R

Repeated Measures ANOVA in R

Linear Models for Repeated Measures ANOVA

Linear Models for Repeated Measures ANOVA

Assumptions of Repeated Measures ANOVA

Normality

Extreme Outliers

Sphericity

Sphericity

Greenhouse-Geisser Correction

Repeated Measures ANOVA in R using ezANOVA()

Repeated Measures ANOVA in R using ezANOVA()

Post-hoc tests

Disadvantages of Repeated Measures ANOVA

Counterbalancing

Latin Square Designs

Latin Square Designs

Differential Carryover Effects

Differential Carryover Effects

Other ANOVA designs

Other ANOVA designs

Other ANOVA designs

Other ANOVA designs

Linear Mixed Effects Models

Go Forth And Do Science!

including `Subjects` reduces the ANOVA error term

including `Subjects` reduces the ANOVA error term

including `Subjects` increases `F`

Repeated Measures ANOVA in R using `ezANOVA()`

Repeated Measures ANOVA in R using `ezANOVA()`