Scientific Computing (Psychology 9040a)

Whereas signals in nature (such as sound waves, magnetic fields, hand position, electromyograms (EMG), electroencephalograms (EEG), extra-cellular potentials, etc) vary continuously, often in science we measure these signals by sampling them repeatedly over time, at some sampling frequency. The resulting collection of measurements is a discretized representation of the original continuous signal.

Before we get into sampling theory however we should first talk about how signals can be represented both in the time domain and in the frequency domain.

Jack Schaedler has a nice page explaining and visualizing many concepts discussed in this chapter:

Time domain representation of signals

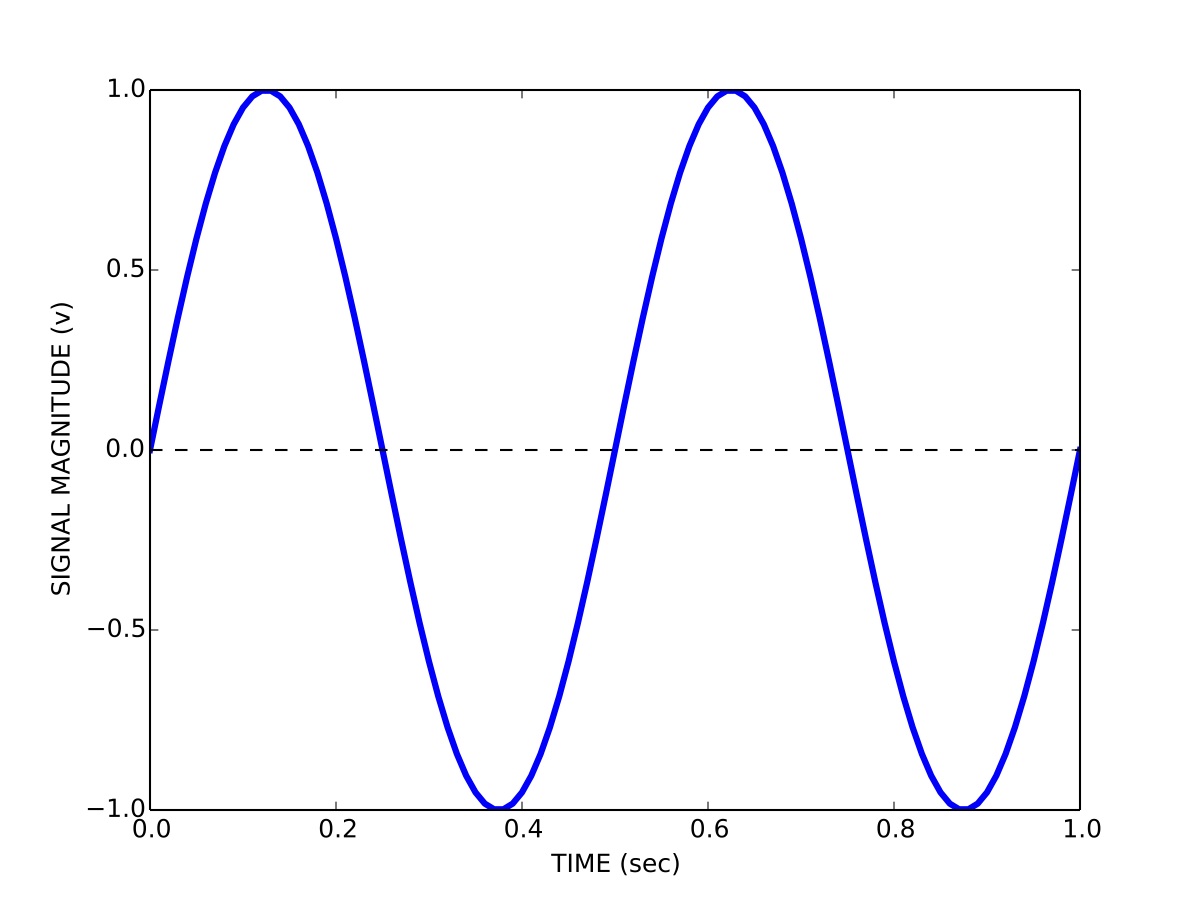
This is how you are probably used to thinking about signals, namely how the magnitude of a signal varies over time. So for example a signal \(s\) containing a sinusoid with a period \(T\) of 0.5 seconds (a frequency of 2 Hz) and a peak-to-peak magnitude \(b\) of 2 volts is represented in the time domain \(t\) as:

We can visualize the signal by plotting its magnitude as a function of time, as shown in Figure 1.

Frequency domain representation of signals

We can also represent signals in the frequency domain. This requires some understanding of the Fourier series. The idea of the Fourier series is that all periodic signals can be represented by (decomposed into) the sum of a set of pure sines and cosines that differ in frequency and period. See the wikipedia link for lots of details and a helpful animation.

\[s(t) = \frac{a_{0}}{2} + \sum_{n=1}^{\infty} \left[a_{n}\mathrm{cos}(nwt) + b_{n}\mathrm{sin}(nwt)\right]\]

The coefficients \(a_{n}\) and \(b_{n}\) define the weighting of the different sines and cosines at different frequencies. In other words these coefficients represent the strength of the different frequency components in the signal.

\[s(t) = \frac{a_{0}}{2} \sum_{n=1}^{\infty} \left[r_{n}\mathrm{cos}(nwt-\phi_{n})\right]\]

Using this formulation we now have magnitude coefficients \(r_{n}\) and phase coefficients \(\phi_{n}\). That is, we are representing the original signal \(s(t)\) using a sum of sinusoids of different frequencies and phases.

Here is a web page that lets you play with how sines and cosines can be used to represent different signals: Fourier series visualization.

Fast Fourier transform (FFT)

Given a signal there is a very efficient computational algorithm called the Fast Fourier transform (FFT) for computing the magnitude and phase coefficients. We will not go into the details of this algorithm here, most high level programming languages have a library that includes the FFT algorithm.

Here is a video showing a 100-year-old mechanical computer that does both forward and inverse Fourier transforms:

Sampling

Before we talk about the FFT and magnitude and phase coefficients, we need to talk about discrete versus continuous signals, and sampling. In theory we can derive a mathematical description of the Fourier decomposition of a continuous signal, as we have done above, in terms of an infinite number of sinusoids. In practice however, signals are not continuous, but are sampled at some discrete sampling rate.

For example, when we use Optotrak to record the position of the fingertip during pointing experiments, we choose a sampling rate of 200 Hz. This means 200 times per second the measurement instrument samples and records the position of the fingertip. The interval between any two samples is 5 ms. It turns out that the sampling rate used has a specific effect on the number of frequencies used in a discrete Fourier representation of the recorded signals.

The Nyquist-Shannon sampling theorem states that a signal must be sampled at a rate which is at least twice that of its highest frequency component. If a signal contains power at frequencies higher than half the sampling rate, these high frequency components will appear in the sampled data at lower frequencies and will distort the recording. This is known as the problem of aliasing.

Let’s look at a concrete example that will illustrate this concept. Let’s assume we have a signal that we want to sample, and we choose a sampling rate of 4 Hz. This means every 250 ms we sample the signal. According to the Shannon-Nyquist theorem, the maximum frequency we can uniquely identify is half that, which is 2 Hz. This is called the nyquist frequency. Let’s look at a plot and see why this is so.

In Figure 2 we see a solid blue line showing a 2 Hz signal, a magenta dashed line showing a 4 Hz signal, and a green dashed line showing a 8 Hz signal. Now imagine we sample these signals at 2 Hz, indicated by the vertical red lines. Notice that at the sample points (vertical red lines), the 2 Hz, 4 Hz and 8 Hz signals overlap with identical values. This means that on the basis of our 2 Hz samples, we cannot distinguish between frequencies of 2, 4 and 8 Hz. What’s more, what this means is that if the signal we are actually sampling at 2 Hz has significant signal power at frequencies above the Nyquist (1 Hz) then the power at these higher frequencies will influence our estimates of the magnitude coefficients corresponding to frequencies below the Nyquist... in other words the high-frequency power will be aliased into the lower frequency estimates.

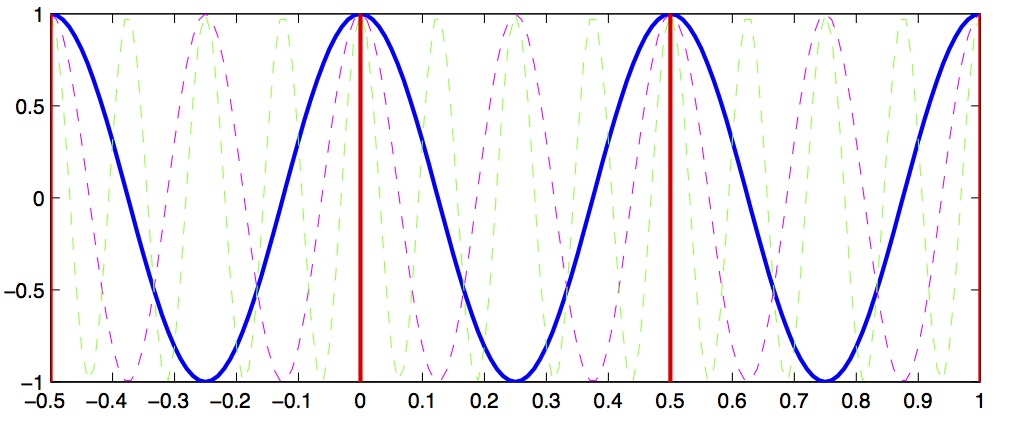
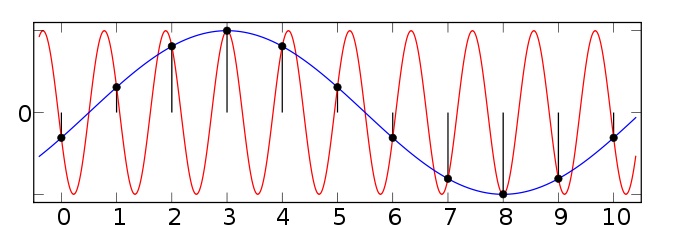
Figure 3 shows another example taken from the wikipedia article on aliasing. Here we have two sinusoids—one at 0.1 Hz (blue) and another at 0.9 Hz (red). We sample both at a sampling rate of 1 Hz (vertical green lines). You can see that at the sample points, both the 0.1 Hz and 0.9 Hz sinusoids pass through the sample points and thus both would influence our estimates of the power at the 0.1 Hz frequency. Since the sampling rate is 1 Hz, the Nyquist frequency (the maximum frequency we can distinguish) is 0.5 Hz—and so any power in the signal above 0.5 Hz (such as 0.9 Hz) will be aliased down into the lower frequencies (in this case into the 0.1 Hz band).

So the message here is that in advance, before choosing your sampling rate, you should have some knowledge about the highest frequency that you (a) are interested in identifying; and (b) you think is a real component in the signal (as opposed to random noise). In cases where you have no a priori knowledge about the expected frequency content, one strategy is to remove high frequency components before sampling. This can be accomplished using low-pass filtering—sometimes called anti-aliasing filters. Once the signal has been sampled, it’s too late to perform anti-aliasing.

Power spectra

Having bypassed completely the computational details of how magnitude and phase coefficients are estimated, we will now talk about how to interpret them.

For a given signal, the collection of magnitude coefficients gives a description of the signal in terms of the strength of the various underlying frequency components. For our immediate purposes these magnitude coefficients will be most important to us and we can for the moment set aside the phase coefficients.

Here is an example of a power spectrum for a pure 10 Hz signal, sampled at 100 Hz.

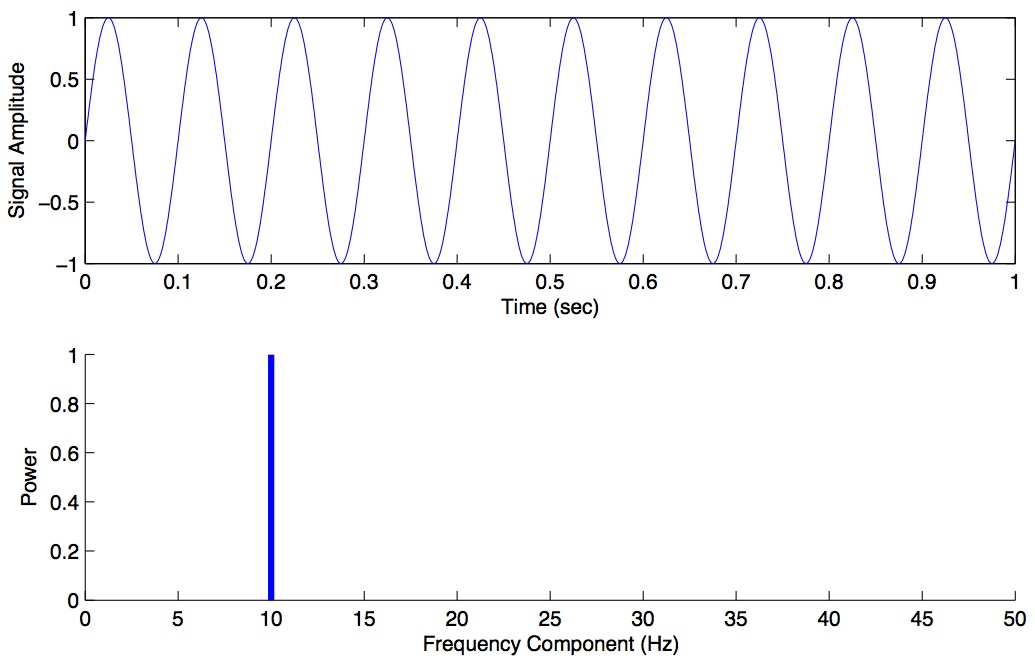
The magnitude values are zero for every frequency except 10 Hz. We haven’t plotted the phase coefficients. The set of magnitude and phase coefficients derived from a Fourier analysis is a complete description of the underlying signal, with one caveat—only frequencies up to the Nyquist are represented. So the idea here is that one can go between the original time-domain representation of the signal and this frequency domain representation of the signal without losing information. As we shall see below in the section on filtering, we can perform operations in the frequency domain and then transform back into the time domain.

Here is some MATLAB code to illustrate these concepts. We construct a one second signal sampled at 100 Hz that is composed of a 6 Hz, 10 Hz and 13 Hz component. We then use the fft() function to compute the Fast Fourier transform, we extract the magnitude information, we set our frequency range (up to the Nyquist) and we plot the spectrum, which is shown in Figure 5.

t = linspace(0,1,100);
y = sin(2*pi*t*6) + sin(2*pi*t*10) + sin(2*pi*t*13);
figure;
subplot(2,1,1)
plot(t,y)
xlabel('Time (sec)')
ylabel('Signal Amplitude')
subplot(2,1,2)
out = fft(y);
mag = abs(real(out));
plot(0:49, mag(1:50));
set(gca,'xlim',[0 50]);
xlabel('Frequency Component (Hz)')
ylabel('Amplitude')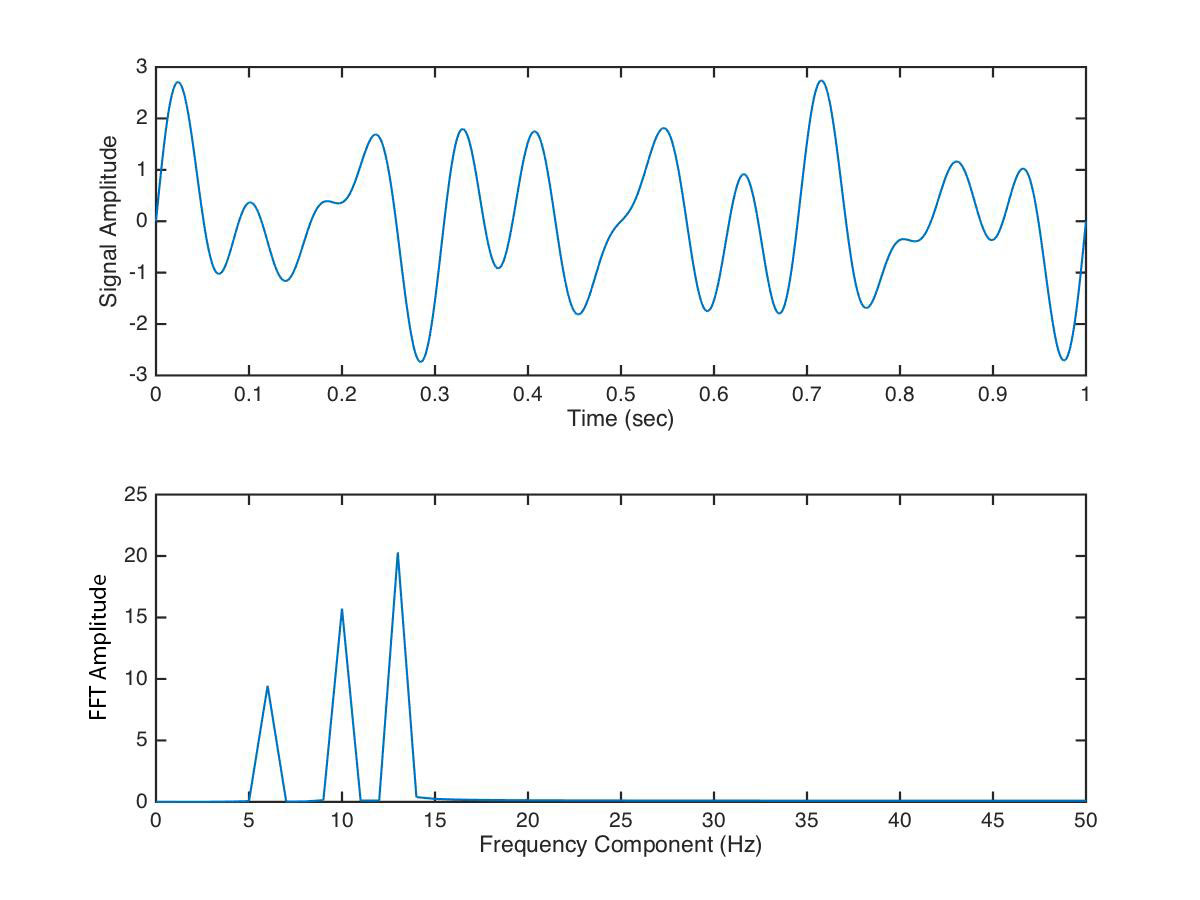

We can see that the power spectrum has revealed peaks at 6, 10 and 13 Hz—which we know is correct, since we designed our signal from scratch.

Typically however signals in the real world that we record are not pure sinusoids, but contain random noise. Noise can originate from the actual underlying process that we are interested in measuring, and it can also originate from the instruments we use to measure the signal. For noisy signals, the FFT taken across the whole signal can be noisy as well, and can make it difficult to see peaks.

Power Spectral Density

One solution is instead of performing the FFT on the entire signal all at once, to instead, split the signal into chunks, take the FFT of each chunk, and then average these spectra to come up with a smoother spectrum. This can be accomplished using a power spectral density function. In MATLAB there is a function pwelch() to accomplish this. We won’t go into the mathematical details or the theoretical considerations (relating to stochastic processes) but for now suffice it to say that the psd can often give you a better estimate of the power at different frequencies compared to a “plain” FFT.

Here is an example of plotting the power spectral density of a signal in MATLAB. We construct a 50 Hz signal at 1000 Hz sampling rate, and we add some random noise on top:

t = linspace(0,1,1000);
y = sin(2*pi*t*50);
yn = y + randn(size(y))*1;
figure
subplot(3,1,1)
plot(t,yn)
xlabel('Time (sec)')
ylabel('Signal Amplitude')
title('TIME SERIES SIGNAL')
subplot(3,1,2)
out = fft(yn);
mag = abs(real(out));
plot(0:499,mag(1:500));
xlabel('Frequency (Hz)')
set(gca,'xlim',[0 100])
ylabel('Power')
title('RAW FFT')
subplot(3,1,3)
pwelch(yn,[],[],[],1000);
set(gca,'xlim',[0 100])
xlabel('Frequency (Hz)')
ylabel('PSD')
title('PSD')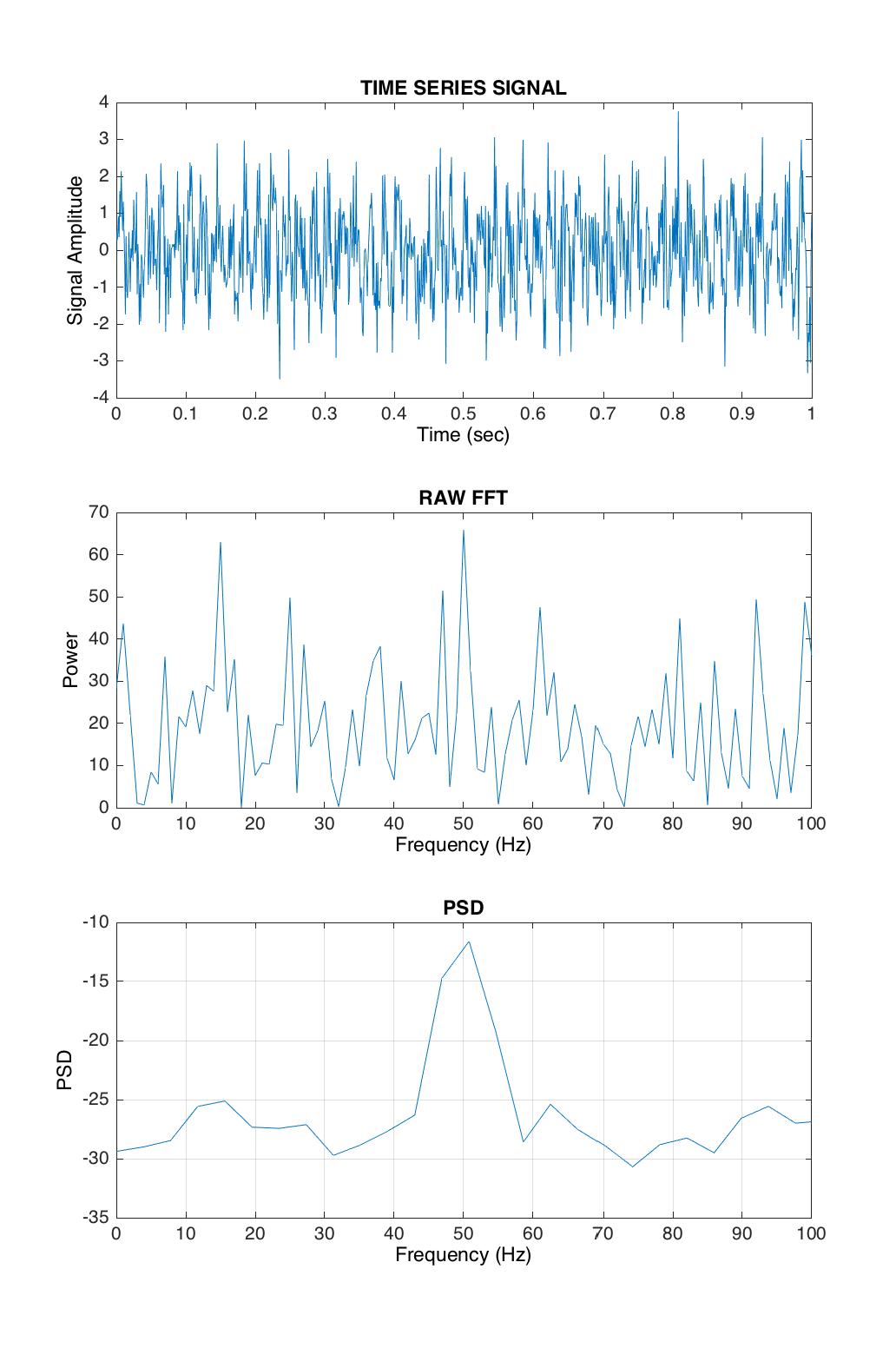

In Figure 6 you can see that the peak at 50 Hz stands nicely above all the noise in the power spectral density estimate (bottom panel), while int the raw FFT it’s difficult to see the 50 Hz peak against the noise (middle panel).

We have been ignoring the phase of the signal here, but just like the magnitude coefficients over frequencies, we can recover the phase coefficients of the signal as well.

Decibel scale

The decibel (dB) scale is a ratio scale. It is commonly used to measure sound level but is also widely used in electronics and signal processing. The dB is a logarithmic unit used to describe a ratio. You will often see power spectra displayed in units of decibels.

The difference between two sound levels (or two power levels, as in the case of the power spectra above), is defined to be:

Thus when \(P_{2}\) is twice as large as \(P_{1}\), then the difference is about 6 dB. When \(P_{2}\) is 10 times as large as \(P_{1}\), the difference is 20 dB. A 100 times difference is 40 dB.

An advantage of using the dB scale is that it is easier to see small signal components in the presence of large ones. In other words large components don’t visually swamp small ones.

Since the dB scale is a ratio scale, to compute absolute levels one needs a reference—a zero point. In acoustics this reference is usually 20 micropascals—about the limit of sensitivity of the human ear.

For our purposes in the absence of a meaningful reference we can use 1.0 as the reference (i.e. as \(P_{1}\) in the above equation).

The pspectrum function in MATLAB

As of 2017 MATLAB introduced a new function called pspectrum() which carries out a more complex algorithm to generate a spectrum of a signal. Here is the help documentation for pspectrum(). The most user-friendly way to start generating spectrums of signals is likely the pspectrum() function. The pwelch() function gives you more fine-grained control and the fft() function is even more granular. My advice is start with pspectrum() unless you have a good reason to do otherwise. The notes and sample problems on the current version of the course still use fft and pwelch and that is fine of course for the demonstration of the concepts.

Spectrogram

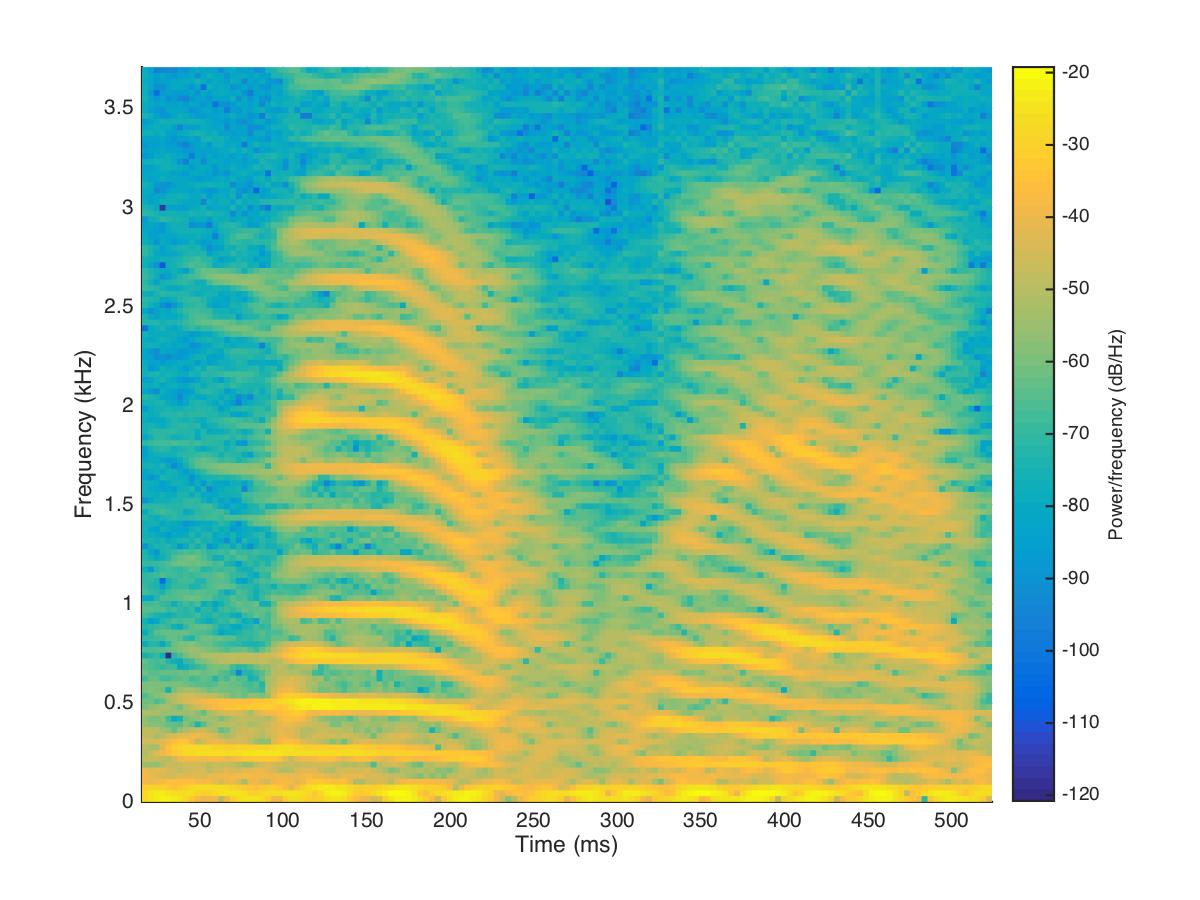
Often there are times when you may want to examine how the power spectrum of a signal (in other words its frequency content) changes over time. In speech acoustics for example, at certain frequencies, bands of energy called formants may be identified, and are associated with certain speech sounds like vowels and vowel transitions. It is thought that the neural systems for human speech recognition are tuned for identification of these formants.

Essentially a spectrogram is a way to visualize a series of power spectra computed from slices of a signal over time. Imagine a series of single power spectra (frequency versus power) repeated over time and stacked next to each other over a time axis.

MATLAB has a built-in function called spectrogram() that will generate a spectrogram. MATLAB has a sample audio file called mtlb.mat which can be loaded from the command line:

load mtlb
spectrogram(mtlb,256,230,256,Fs,'yaxis')
sound(mtlb)

Figure 7 shows the resulting spectrogram. Time is on the horizontal axis and frequency is on the vertical axis. The colours indicate the power of the different frequencies at the given time points.

Filtering

The Fourier series representation and its computational implementation, the FFT and the PSD, are useful not only for determining what frequency components are present in a signal, but we can also perform operations within frequency space in order to manipulate the strength of different frequency components in the signal. This can be especially effective for eliminating noise sources with known frequency content.

t = linspace(0,1,1000);
y = sin(2*pi*t*6) + sin(2*pi*t*10) + sin(2*pi*t*13);
yn = y + randn(size(y))*0.5;
[f,x,y] = fft_plus(yn,1000);
semilogx(f,20*log10(x));
xlabel('Frequency (Hz)')
ylabel('Power (dB)')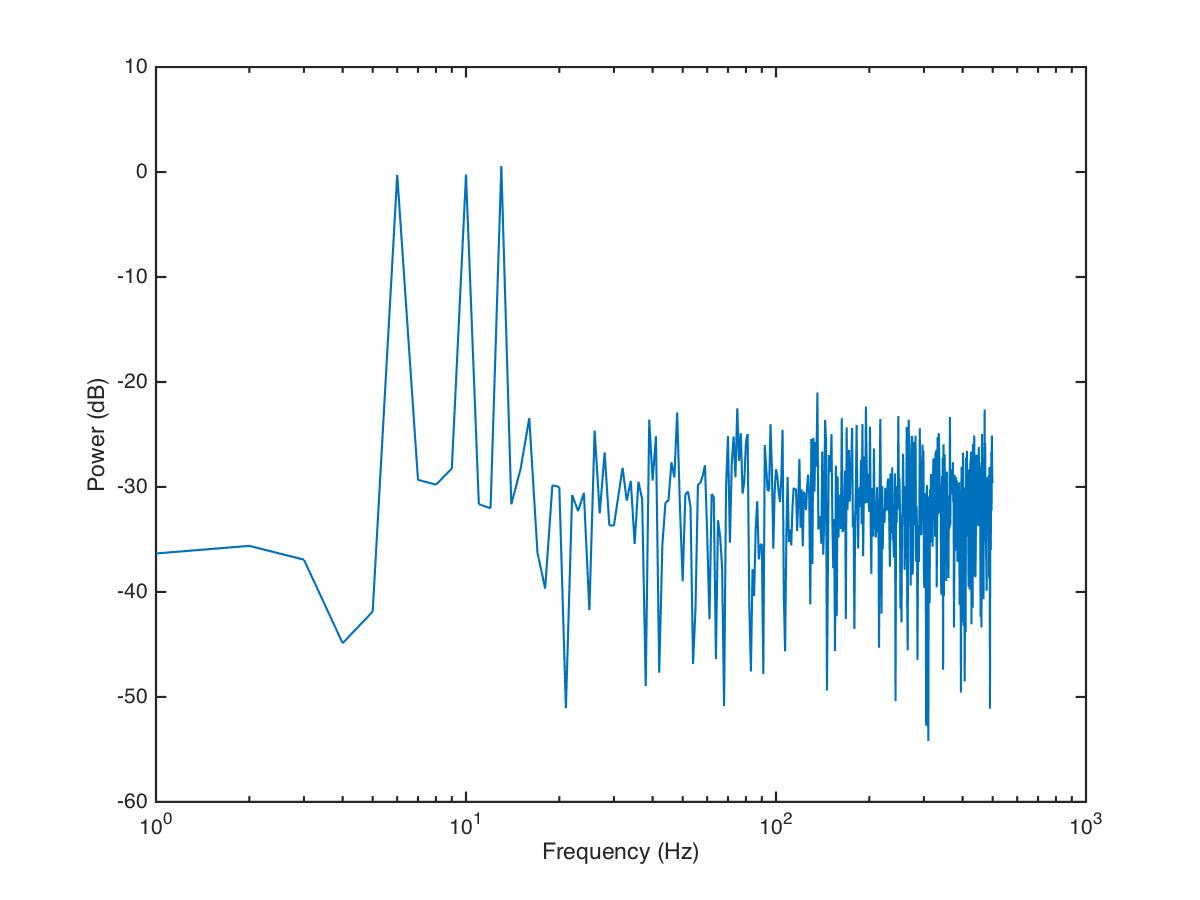

In Figure 8 we can see the signal has three signal components: 6, 10 and 13 Hz. Let’s say we believe that the frequencies we are interested in are all below 20 Hz. In other words, frequencies above that are assumed to be noise of one sort or another. We can filter the signal so that all frequencies above 20 Hz are essentially zeroed out (or at least reduced in magnitude). One way to do this is simply to take the vector of power coefficients, change all values for frequencies above 20 Hz to zero, and perform an inverse Fourier transform (the inverse of the FFT) to go back to the time domain. We won’t go into the mathematical details, but there are also other ways to filter a signal as well.

In the code example above we use a function called fft_plus, which conveniently performs the FFT and converts the results into a format that is useful. Here is the function:

function [f, m, p] = fft_plus (x, Fs)
%
% from https://www.mathworks.com/help/signal/examples/practical-introduction-to-frequency-domain-analysis.html
% function [f, m, p] = fft_plus (x, Fs)
% inputs: x = signal, Fs = sampling rate (Hz)
% outputs: f = frequency, m = magnitude, p = phase

L = length(x);

Y = fft(x,L);

f = ((0:1/L:1-1/L)*Fs).';

m = abs(Y);        % Magnitude of the FFT
p = unwrap(angle(Y));  % Phase of the FFT

f = f(1:floor(L/2));
m = m(1:floor(L/2));
p = p(1:floor(L/2));

end

Characterizing filter performance

A useful way of characterizing a filter’s performance is in terms of the ratio of the amplitude of the output to the input (the amplitude ratio AR or gain), and the phase shift (\(\phi\)) between the input and output, as functions of frequency. A plot of the amplitude ratio and phase shift against frequency is called a Bode plot.

The pass band of a filter is the range of frequencies over which signals pass with no change. The stop band refers to the range of frequencies over which a filter attenuates signals. The cutoff frequency or corner frequency of a filter is used to describe the transition point from the pass band to the reject band. This this transition cannot occur instantaneously it is usually defined to be the point at which the filter output is equal to -6 dB of the input in the pass band. The cutoff frequency is sometimes called the -6 dB point or the half-power point since -6 dB corresponds to half the signal power. The roll-off refers to the rate at which the filter attenuates the input after the cutoff point. When the roll-off is linear it can be specified as a specific slope, e.g. in terms of dB/decade or dB/octave (an octave is a doubling in frequency).

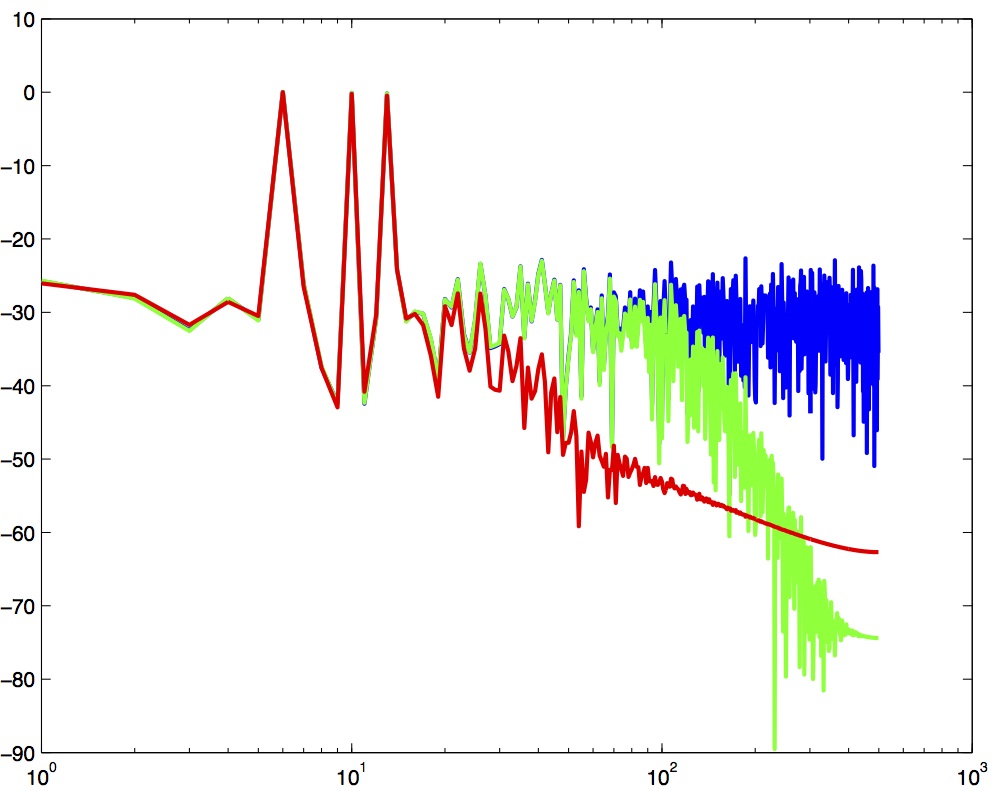
In Figure 9 the blue trace shows the power spectrum for the unfiltered signal. The red trace shows a lowpass-filtered version of the signal with a cutoff frequency of 30 Hz. The green trace shows a low-pass with a cutoff frequency of 130 Hz. Also notice that the roll-off of the 30 Hz lowpass is not as great as for the 130 Hz lowpass, which has a higher roll-off.

In my version of MATLAB (2018b) the Signal Processing Toolbox now includes built-in functions for lowpass, highpass, bandpass and bandstop filtering. If you have an older version of MATLAB that doesn’t include these, I have written some custom functions below that you can use to perform filtering.

function newdata = PLGlowpass(data,samprate,cutoff,order)

% newdata = lowpass(data,samprate,cutoff,order)
%
% performs a lowpass filtering of the input data
% using an nth order zero phase lag butterworth filter

if nargin==3 order=2; end; % default to 2nd order

% get filter paramters A and B
[B,A] = butter(order,cutoff/(samprate/2));
% perform filtering
newdata = filtfilt(B,A,data);

function newdata = PLGhighpass(data,samprate,cutoff,order)

% newdata = highpass(data,samprate,cutoff,order)
%
% performs a highpass filtering of the input data
% using an nth order zero phase lag butterworth filter

if nargin==3 order=2; end;

[B,A] = butter(order,cutoff/(samprate/2),'high');

newdata = filtfilt(B,A,data);

function newdata = PLGbandpass(data,samprate,cutoff,order)

% newdata = bandpass(data,samprate,cutoff,order)
%
% performs a bandpass filtering of the input data
% using an nth order zero phase lag butterworth filter

if nargin==3 order=2; end;

[B,A] = butter(order/2,cutoff./(samprate/2));

newdata = filtfilt(B,A,data);

function newdata = PLGbandstop(data,samprate,cutoff,order)

% newdata = bandstop(data,samprate,cutoff,order)
%
% performs a bandstop filtering of the input data
% using an nth order zero phase lag butterworth filter

if nargin==3 order=2; end;

[B,A] = butter(order/2,cutoff./(samprate/2),'stop');

newdata = filtfilt(B,A,data);

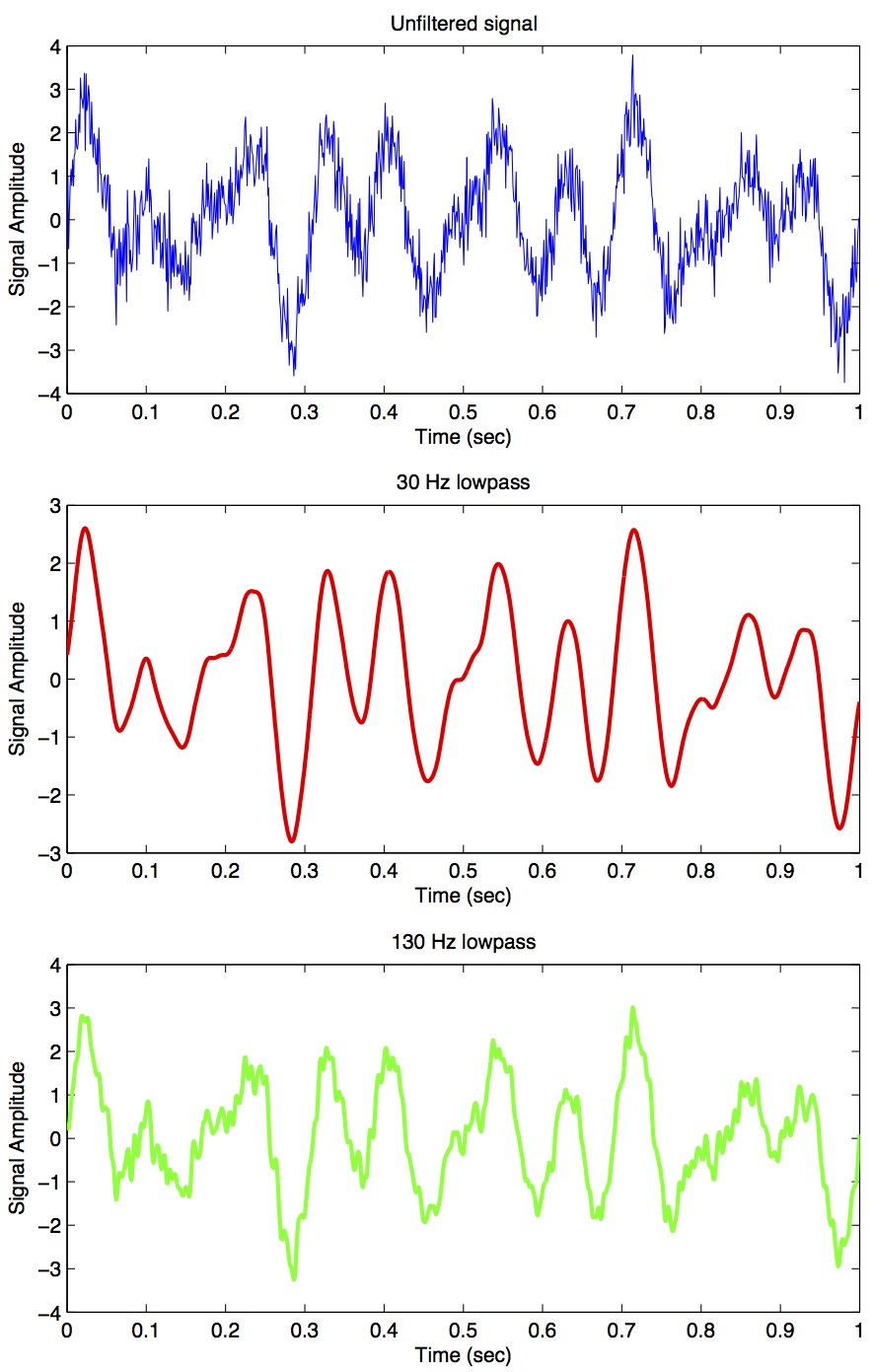
In the code we use a two-pass, bi-directional filter function (called filtfilt()) to apply the butterworth filter to the signal. One-way single-pass filter functions (e.g. filter()) introduce time lags. This is why in real-time applications in which you want to filter signals in real time (e.g. to reduce noise) there are time lags introduced.

So we see a very good example of how low-pass filtering can be used very effectively to filter out random noise. Key is the appropriate choice of cut-off frequency.

Common Filters

There are many different designs of filters, each with their own characteristics (gain, phase and delay characteristics). Some common types:

Filter order

In filter design the order of a filter is one characteristic that you might come across. Technically the definition of the filter order is the highest exponent in the z-domain (transfer function) of a digital filter. That’s helpful isn’t it! (not) Another way of describing filter order is the degree of the approximating polynomial for the filter. Yet another way of describing it is that increasing the filter order increases roll-off and brings the filter closer to the ideal response (i.e. a “brick wall” roll-off).

Practically speaking, you will find that a second-order butterworth filter provides a nice sharp roll-off without too much undesirable side-effects (e.g. large time lag, ripple in the pass-band, etc).

See this section of the wikipedia page on low-pass filters for another description.

High-frequency noise and taking derivatives

One of the characteristics of just about any experimental measurement is that the signal that you measure with your instrument will contain a combination of true signal and “noise” (random variations in the signal). A common approach is to take many measurements and average them together. This is what is commonly done in EEG/ERP studies, in EMG studies, with spike-triggered averaging, and many others. The idea is that if the “real” part of the signal is constant over trials, and the “noise” part of the signal is random from trial to trial, then averaging over many trials will average out the noise (which is sometimes positive, sometimes negative, but on balance, zero) and what remains will be the true signal.

You can imagine however that there are downsides to this approach. First of all, it requires that many, many measures be taken so that averages can be computed. Second, there is no guarantee that the underlying “true” signal will in fact remain constant over those many measurements. Third, one cannot easily do analyses on single trials, since we have to wait for the average before we can look at the data.

One solution is to use signal processing techniques such as filtering to separate the noise from the signal. A limitation of this technique however is that when we apply a filter (for example a low-pass filter), we filter out all power in the signal above the cutoff frequency—whether “real” signal or noise. This approach thus assumes that we are fairly certain that the power above our cutoff is of no interest to us.

One salient reason to low-pass filter a signal, and remove high-frequency noise, is for cases in which we are interested in taking the temporal derivative of a signal. For example, let’s say we have recorded the position of the fingertip as a subject reaches from a start position on a tabletop, to a target located in front of them on a computer screen. Using a device like Optotrak we can record the (x,y,z) coordinates of the fingertip at a sampling rate of 200 Hz. Figure 11 shows an example of such a recording.

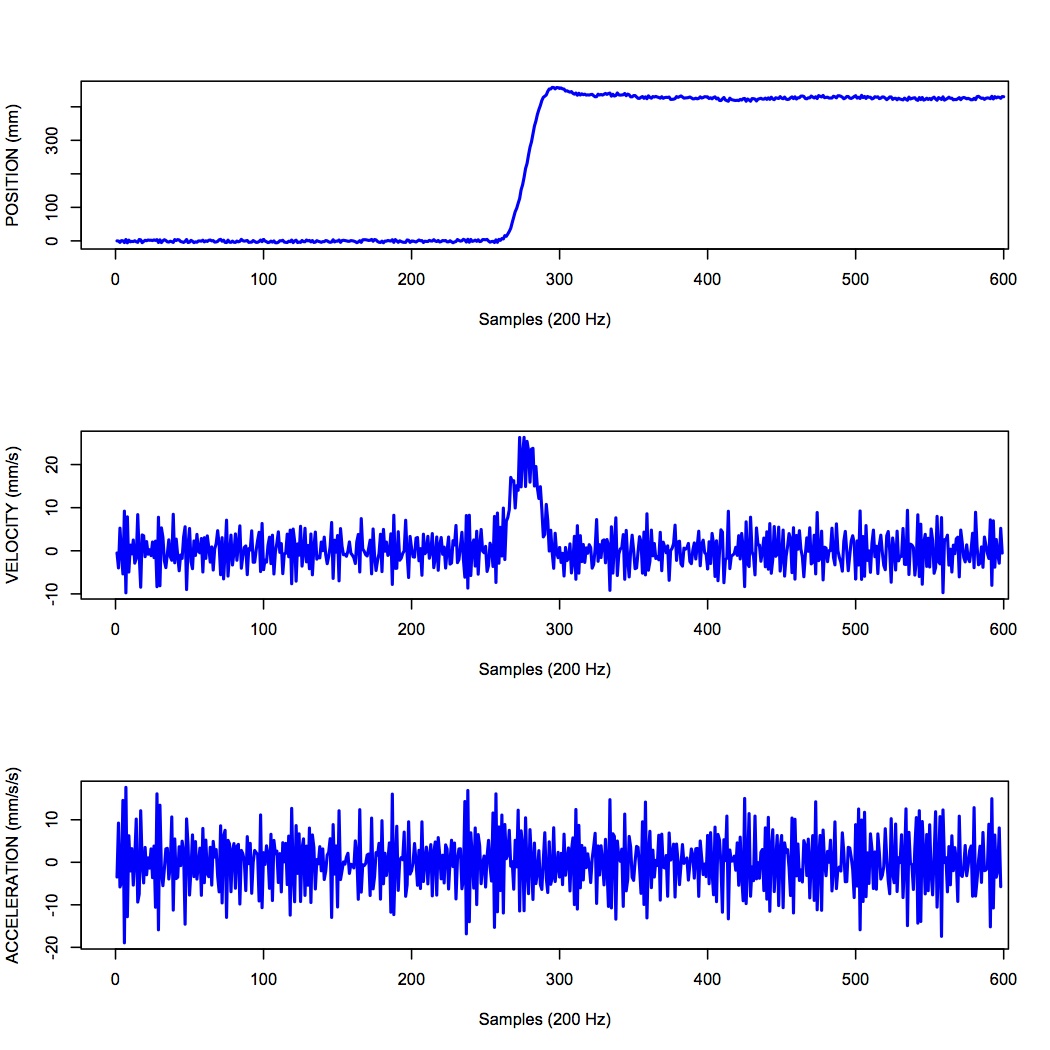
In Figure 11 the top panel shows position in one coordinate over time. The middle panel shows the result of taking the derivative of the position signal to obtain velocity. I have simply used the diff() function here to obtain a numerical estimate of the derivative, taking the forward difference. Note how much noisier it looks than the position signal. Finally the bottom panel shows the result of taking the derivative of the velocity signal, to obtain acceleration. It is so noisy one cannot even see the peaks in the acceleration signal, they are completely masked by noise.

What is happening here is that small amounts of noise in the position signal are amplified each time a derivative is taken. One solution is to low-pass filter the position signal. The choice of the cutoff frequency is key—too low and we will decimate the signal itself, and too high and we will not remove enough of the high frequency noise. It happens that we are fairly certain in this case that there isn’t much real signal power above 12 Hz for arm movements. Figure 12 shows what it looks like when we low-pass filter the position signal at a 12Hz cutoff frequency.

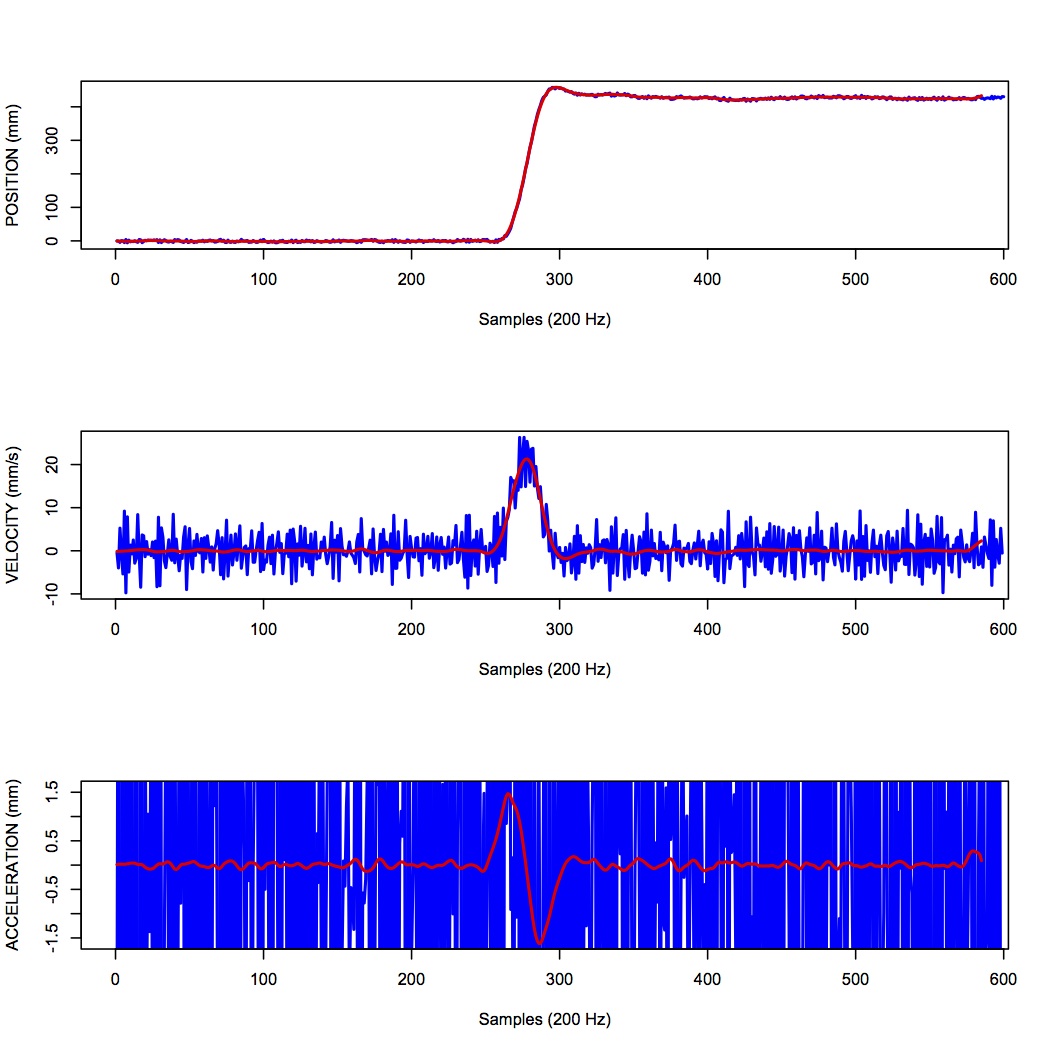
What you can see in Figure 12 is that for the position over time, the filtered version (shown in red) doesn’t differ that much, at least not visibly, from the unfiltered version (in blue). The velocity and acceleration traces however look vastly different. Differentiating the filtered position signal yields a velocity trace (shown in red in the middle panel) that is way less noisy than the original version. Taking the derivative again of this new velocity signal yields an acceleration signal (shown in red in the bottom panel) that is actually usable. The original version (shown in blue) is so noisy it overwhelms the entire panel. Note the scale change on the ordinate.

Quantization

Converting an analog signal to a digital form involves the quantization of the analog signal. In this procedure the range of the input variable is divided into a set of class intervals. Quantization involves the replacement of each value of the input variable by the nearest class interval centre.

Another way of saying this is that when sampling an analog signal and converting it to digital values, one is limited by the precision with which one can represent the (analog) signal digitally. Usually a piece of hardware called an analog-to-digital (A/D) board is the thing that performs this conversion. The range of A/D boards are usually specified in terms of bits. For example a 12-bit A/D board is capable of specifying \(2^{12}=4096\) unique values. This means that a continuous signal will be represented using only 4096 possible values. A 16-bit A/D board would be capable of using \(2^{16}=65,536\) different values. Obviously the higher the better, in terms of the resolution of the underlying digital representation. Often however in practice, higher resolutions come at the expense of lower sampling rates.

As an example, let’s look at a continuous signal and its digital representation using a variety of (low) sample resolutions. Figure 13 shows a range of sample resolutions.

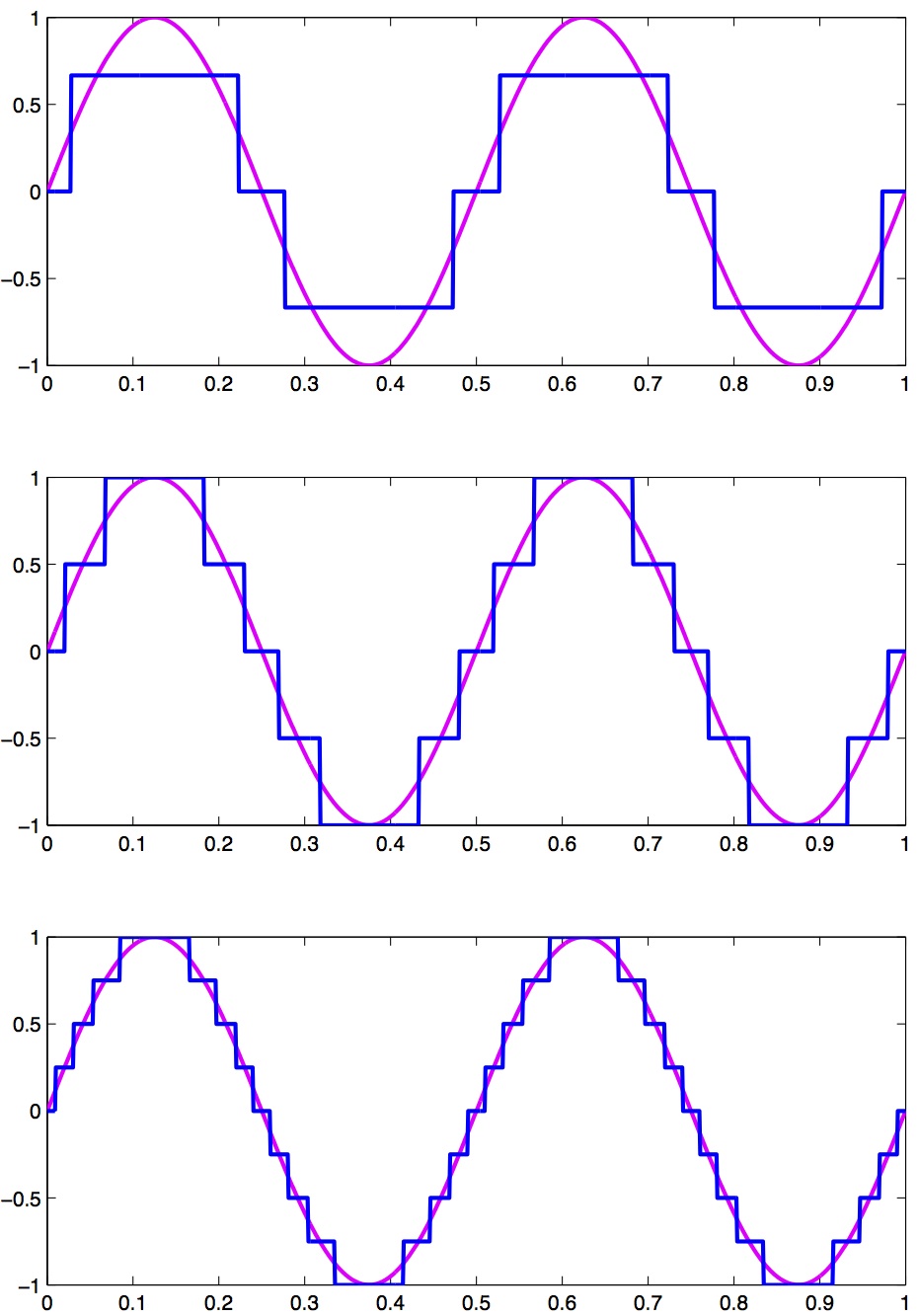
Here we see as the number of possible unique values increases, the digital representation of the underlying continuous signal gets more and more accurate. Also notice that in general, quantization adds noise to the representation of the signal.

It is also important to consider the amplitude of the sampled signal compared to the range of the A/D board. In other words, if the signal you are sampling has a very small amplitude compared to the range of the A/D board then essentially your sample will only be occupying a small subset of the total possible values dictated by the resolution of the A/D board, and the effects of quantization will be greatly increased.

For example, let’s say you are using an A/D board with 12 bits of resolution and an input range of +/- 5 Volts. This means that you have \(2^{12}=4096\) possible values with which to characterize a signal that ranges maximally over 10 Volts. If your signal is very small compared to this range, e.g. if it only occupies 25 millivolts, then the A/D board is only capable of using \(0.0025/10*4096=10\) (ten) unique values to characterize your signal! The resulting digitized characterization of your signal will not be very smooth.

Whenever possible, amplify your signal to occupy the maximum range of the A/D board you’re using. Of course the trick is always to amplify the signal without also amplifying the noise!

Sources of noise

It is useful to list a number of common sources of noise in physiological signals:

Scientific Computing (Psychology 9040a)

Signals, Sampling, & Filtering

Time domain representation of signals

Frequency domain representation of signals

Fast Fourier transform (FFT)

Sampling

Power spectra

Power Spectral Density

Decibel scale

The `pspectrum` function in MATLAB

Spectrogram

Filtering

Characterizing filter performance

Common Filters

Filter order

High-frequency noise and taking derivatives

Quantization

Sources of noise

Signals, Sampling, & Filtering

Time domain representation of signals

Frequency domain representation of signals

Fast Fourier transform (FFT)

Sampling

Power spectra

Power Spectral Density

Decibel scale

The pspectrum function in MATLAB

Spectrogram

Filtering

Characterizing filter performance

Common Filters

Filter order

High-frequency noise and taking derivatives

Quantization

Sources of noise

The `pspectrum` function in MATLAB