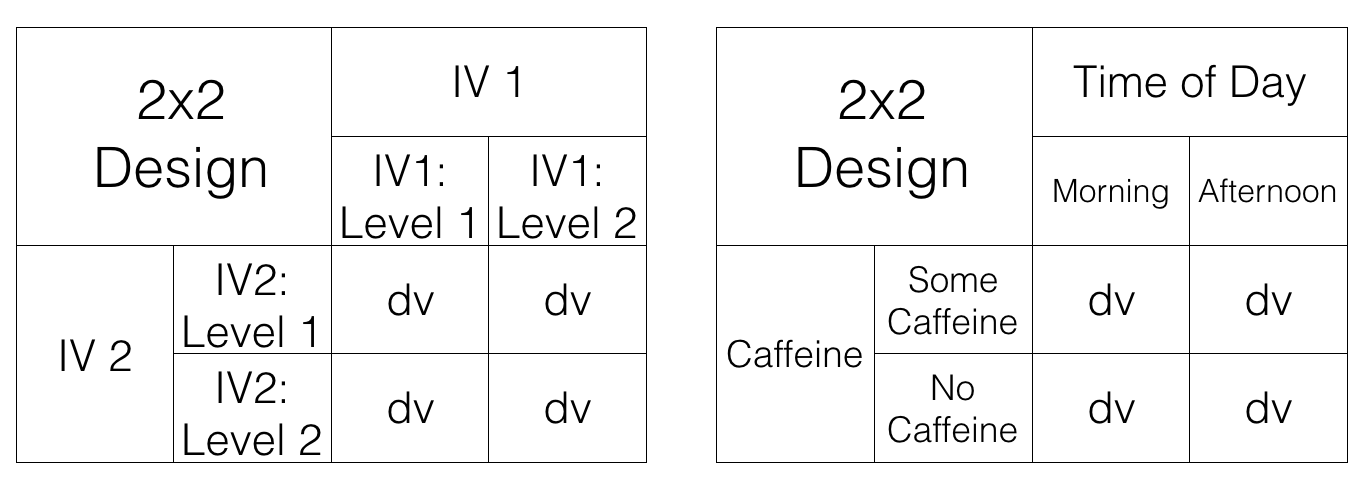
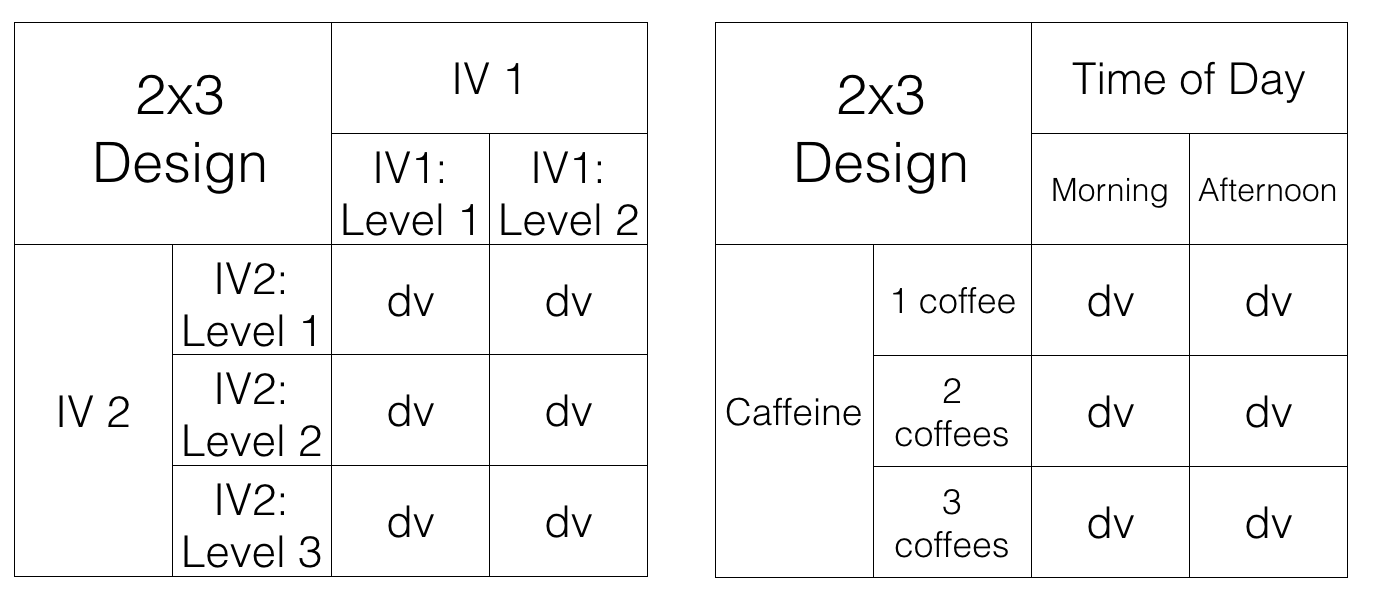
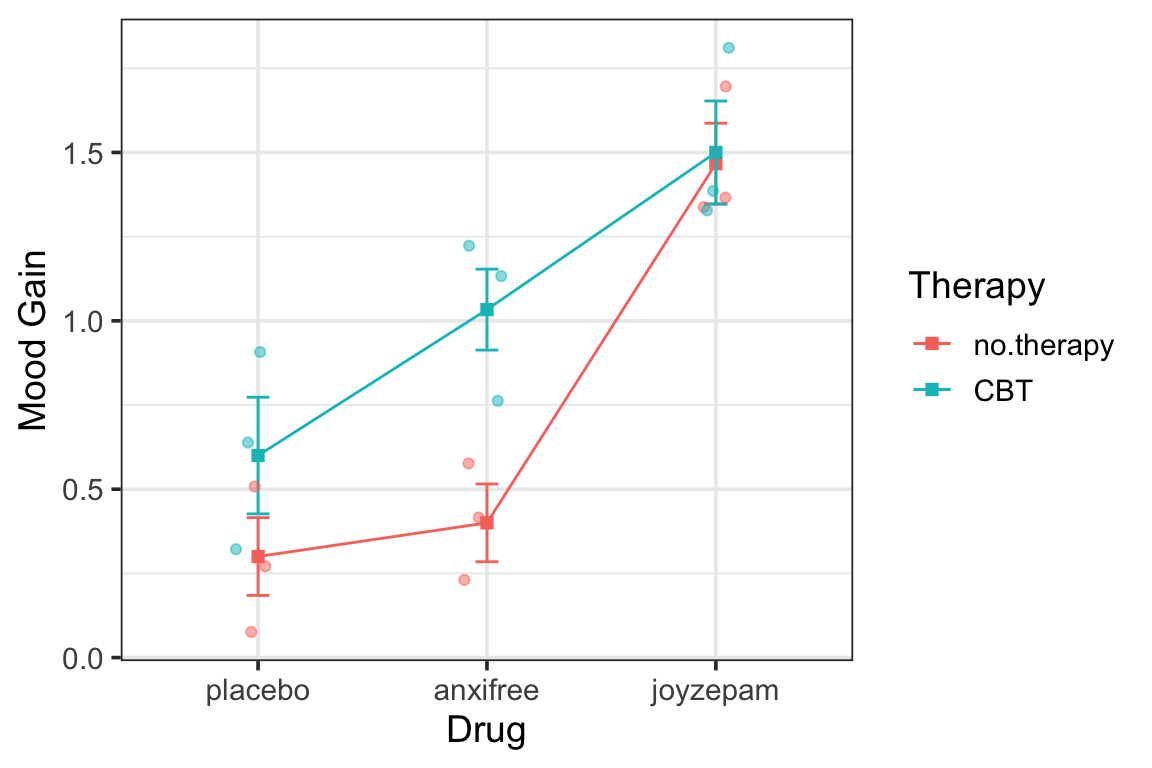
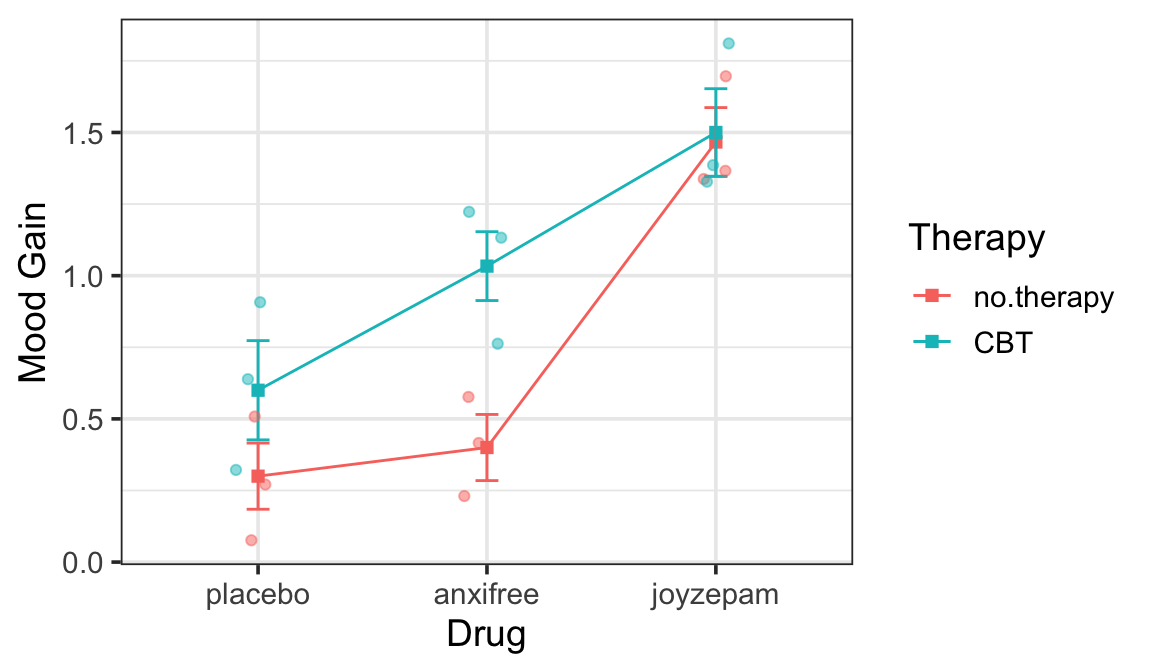
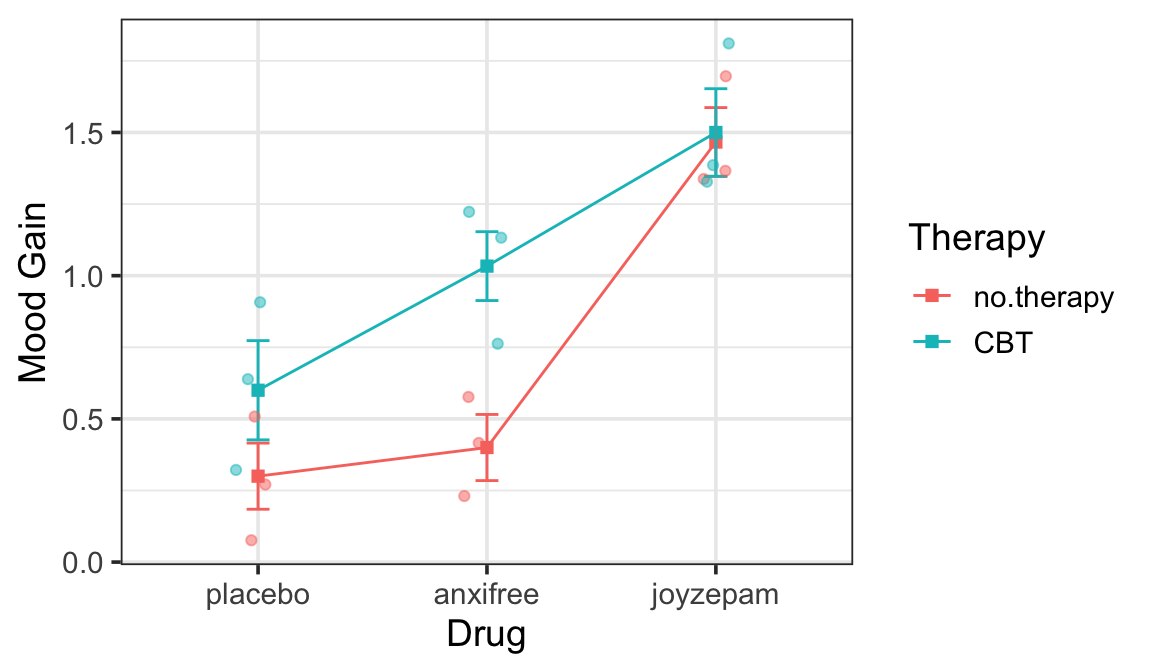
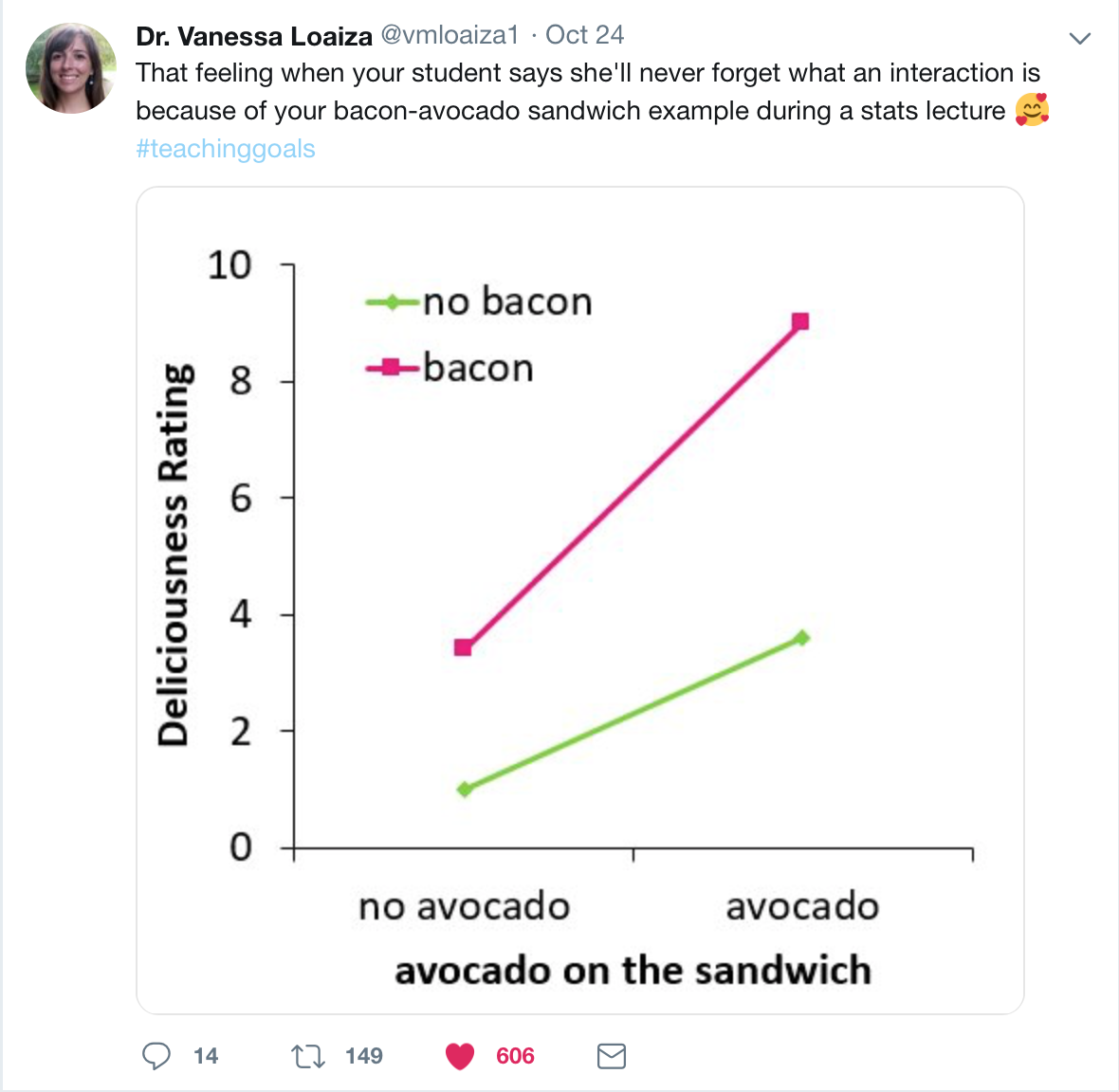
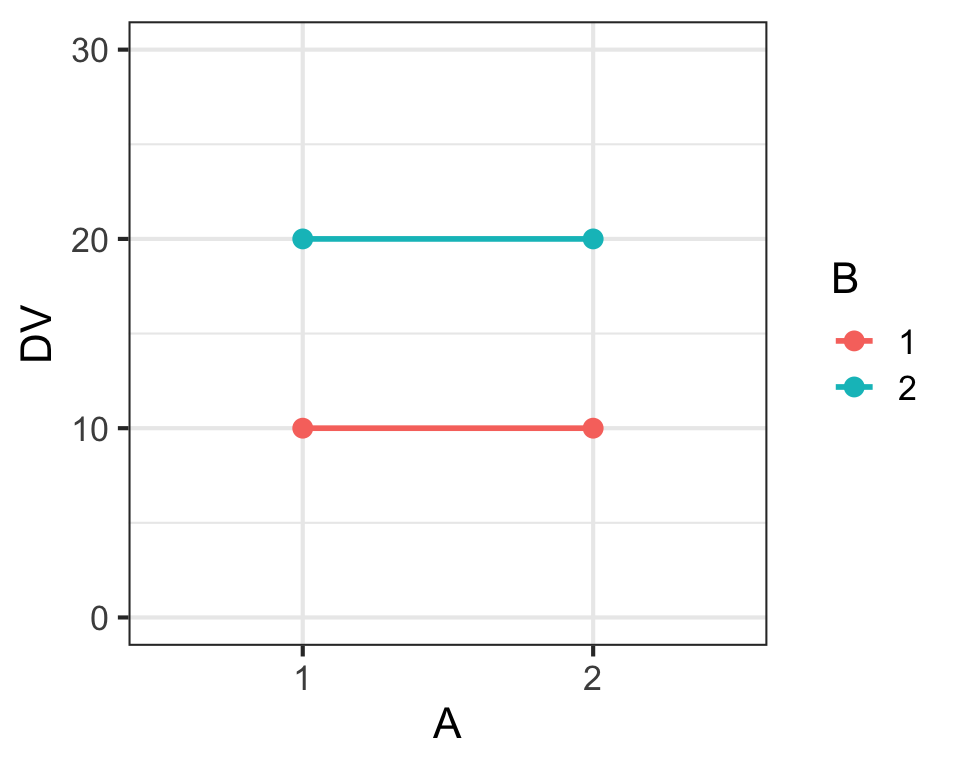
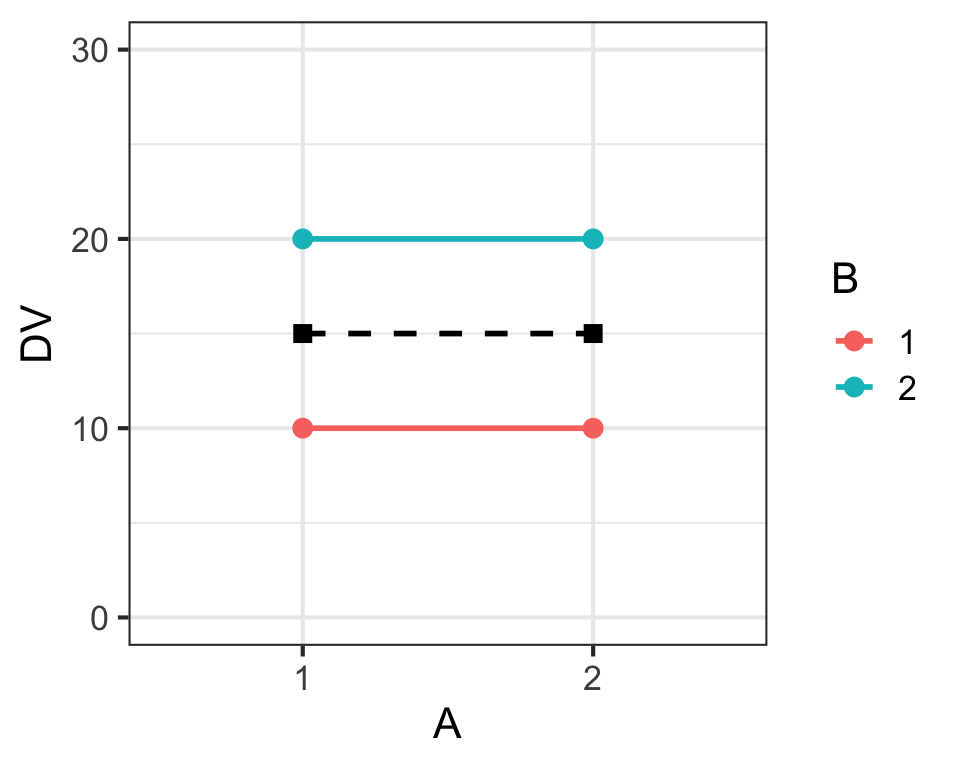
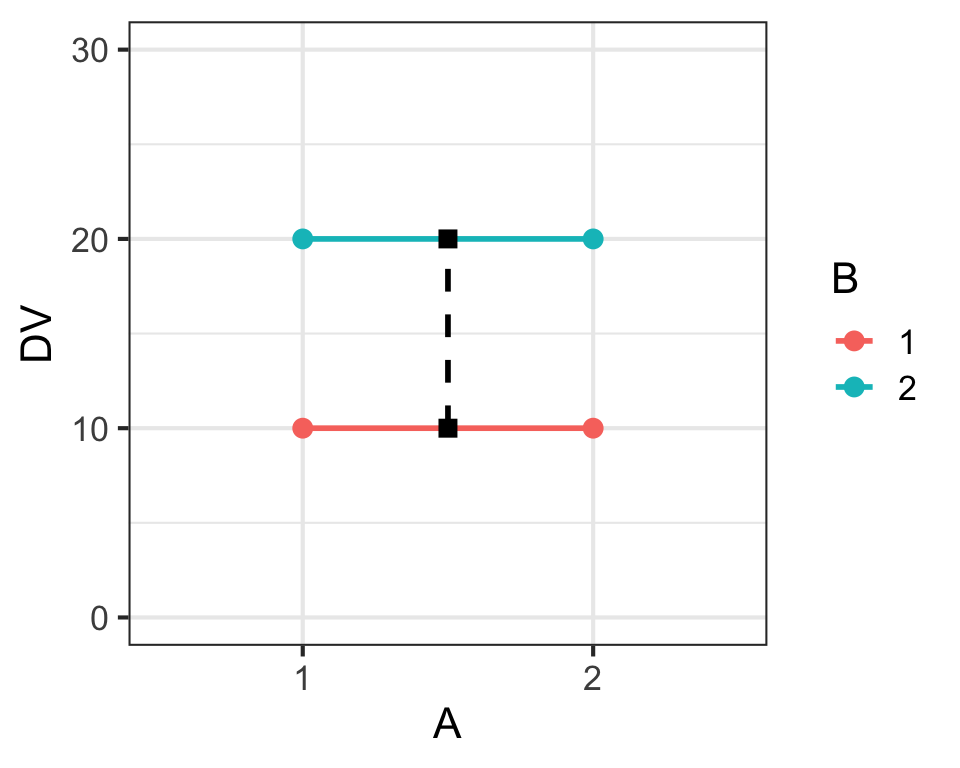
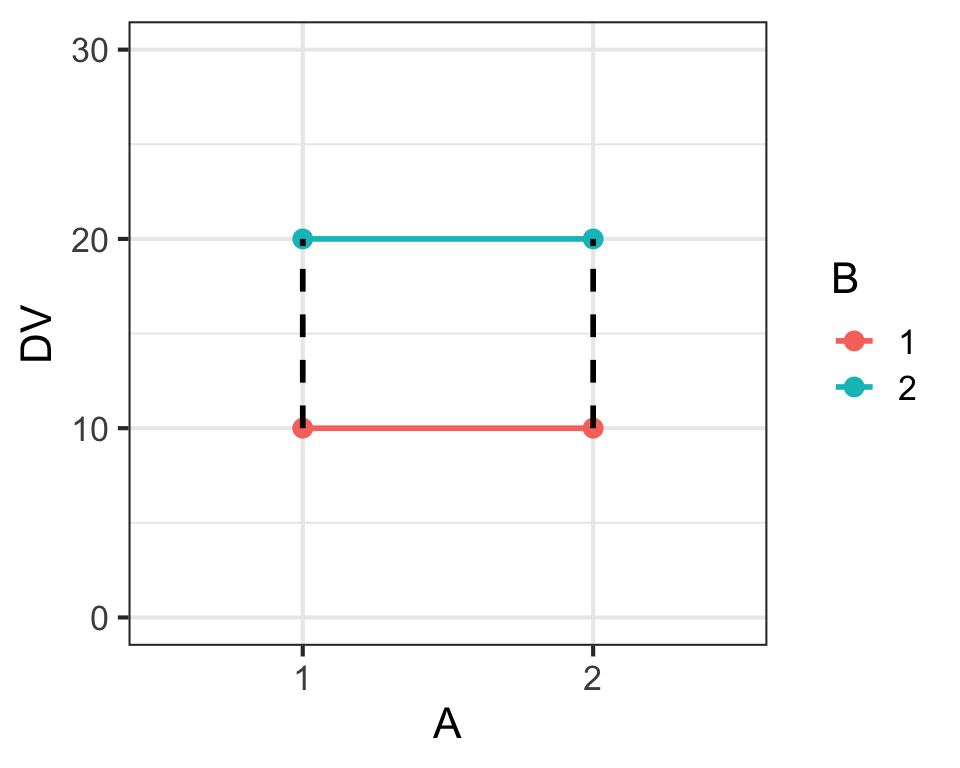
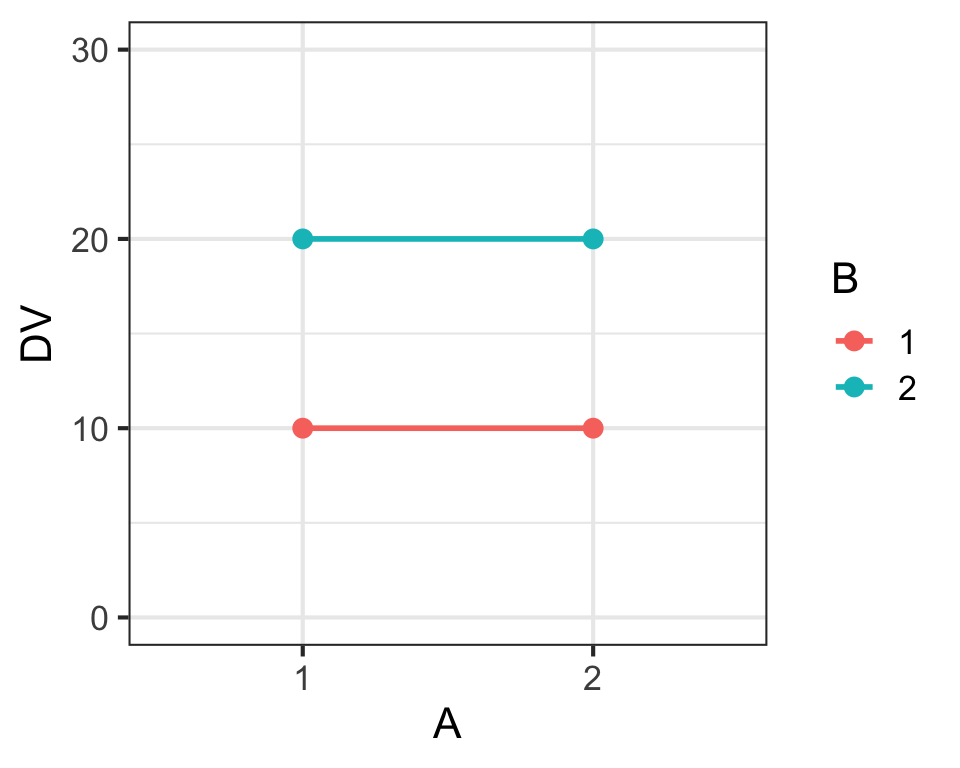
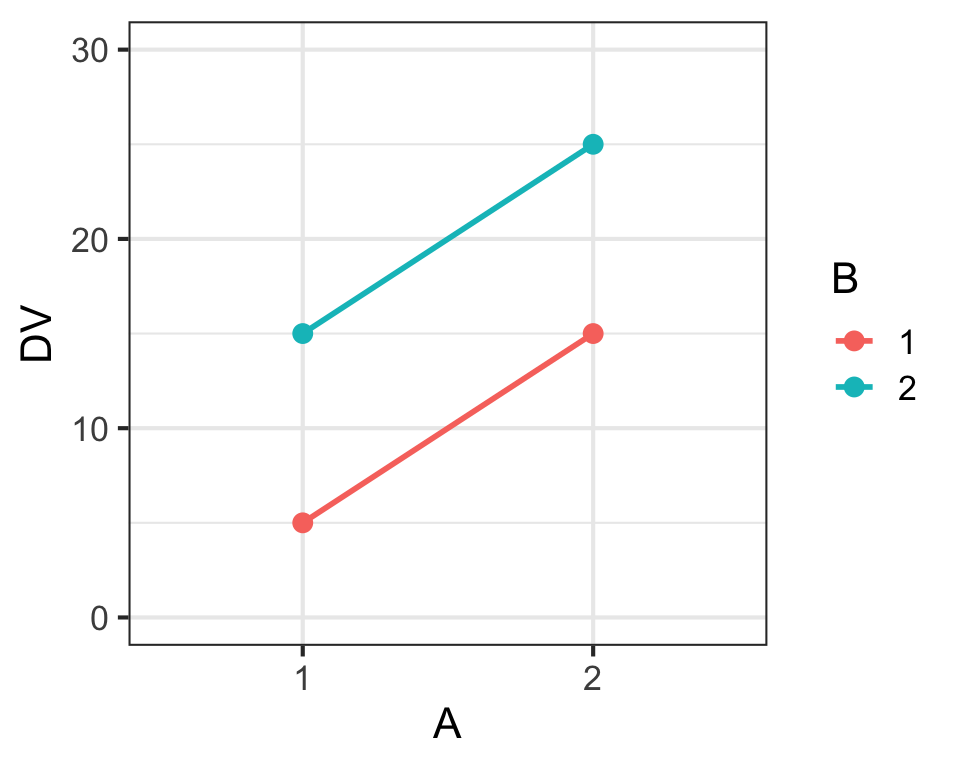
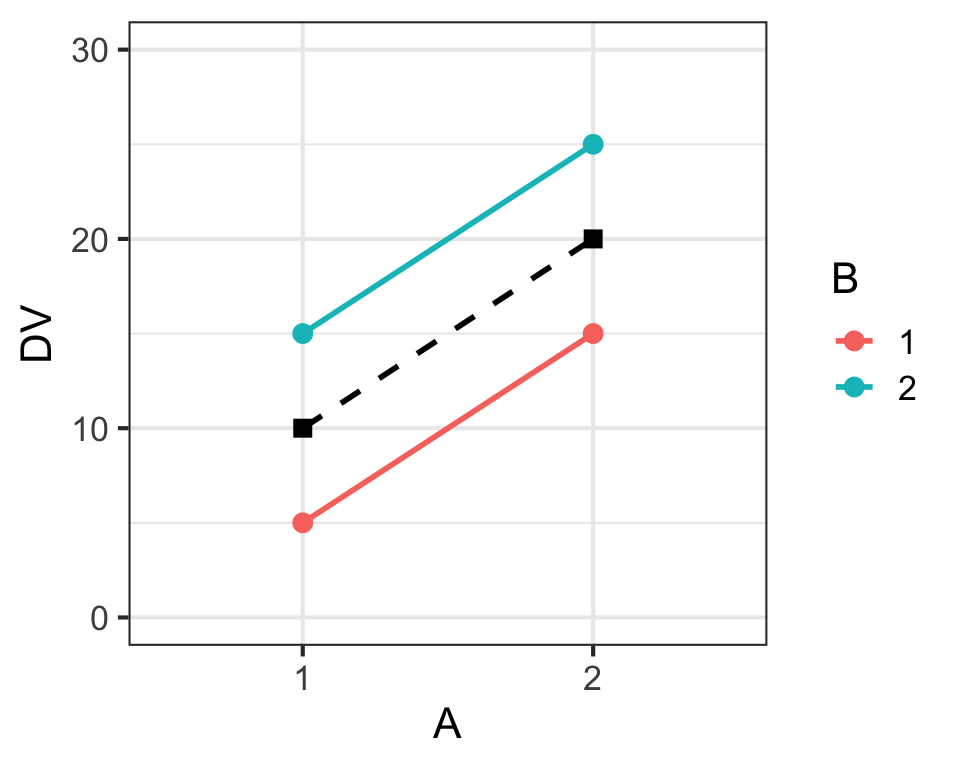
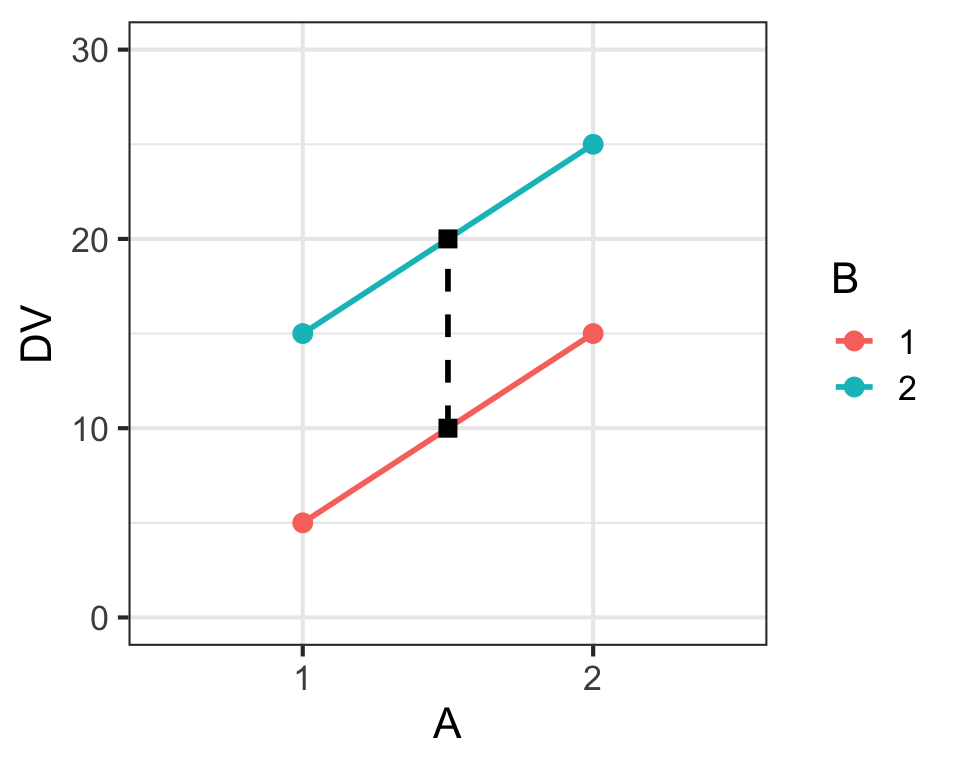
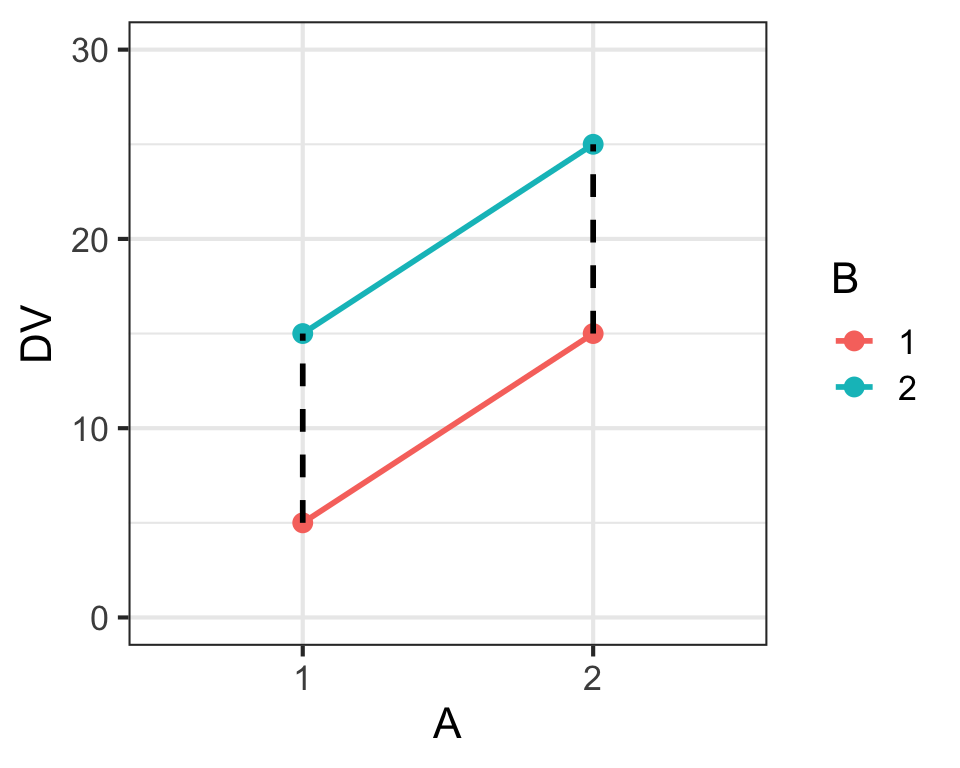
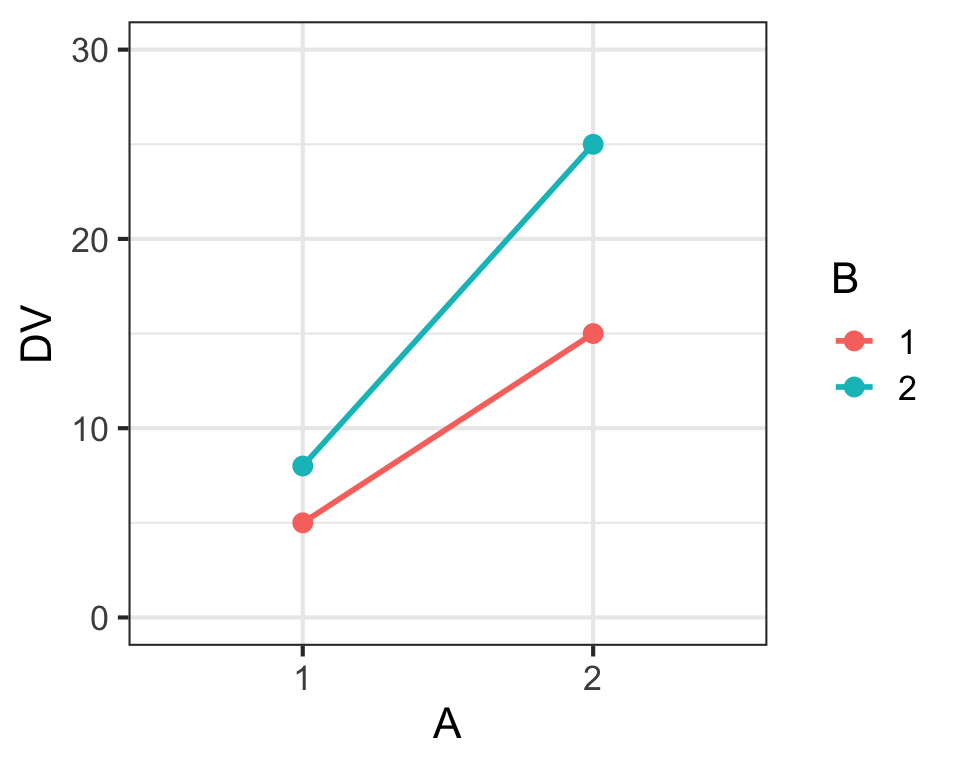
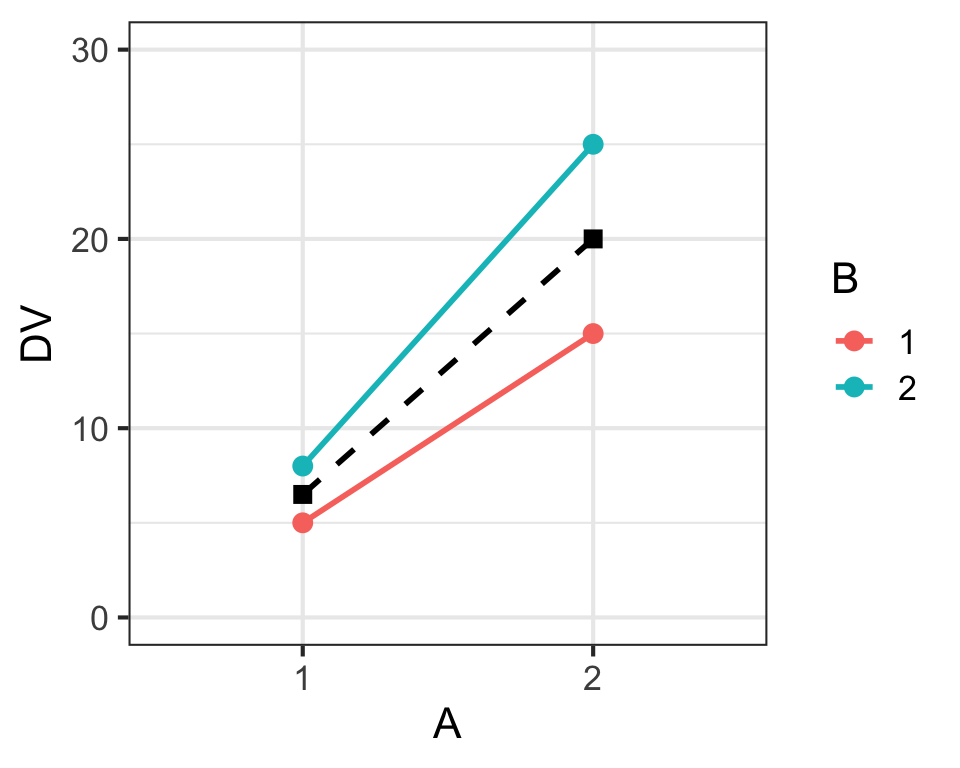
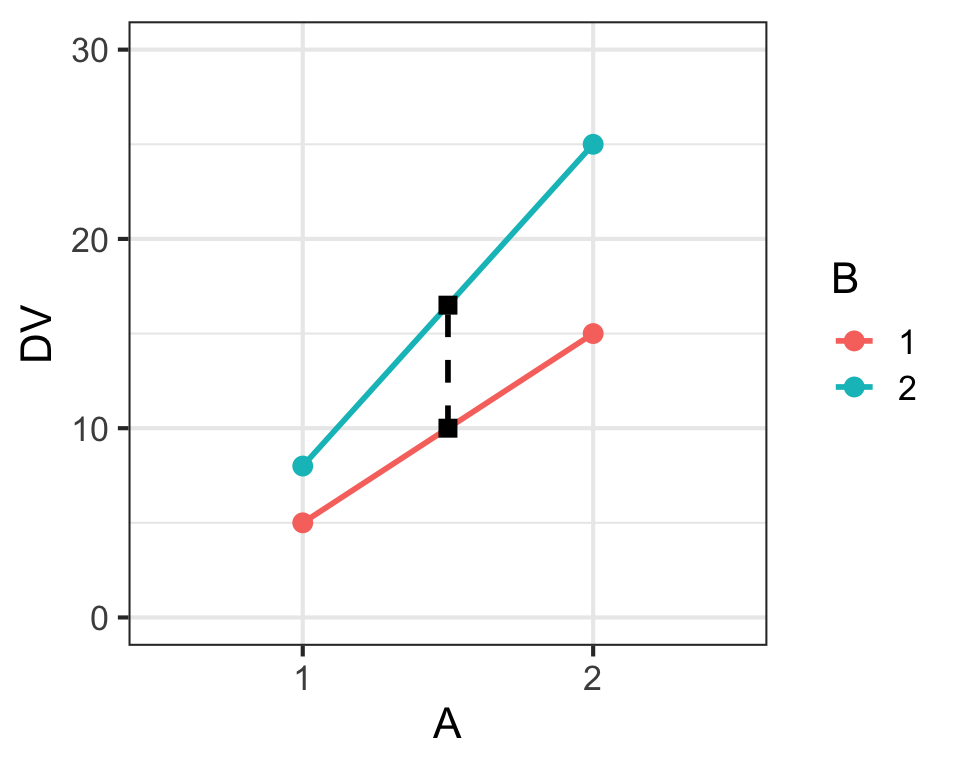
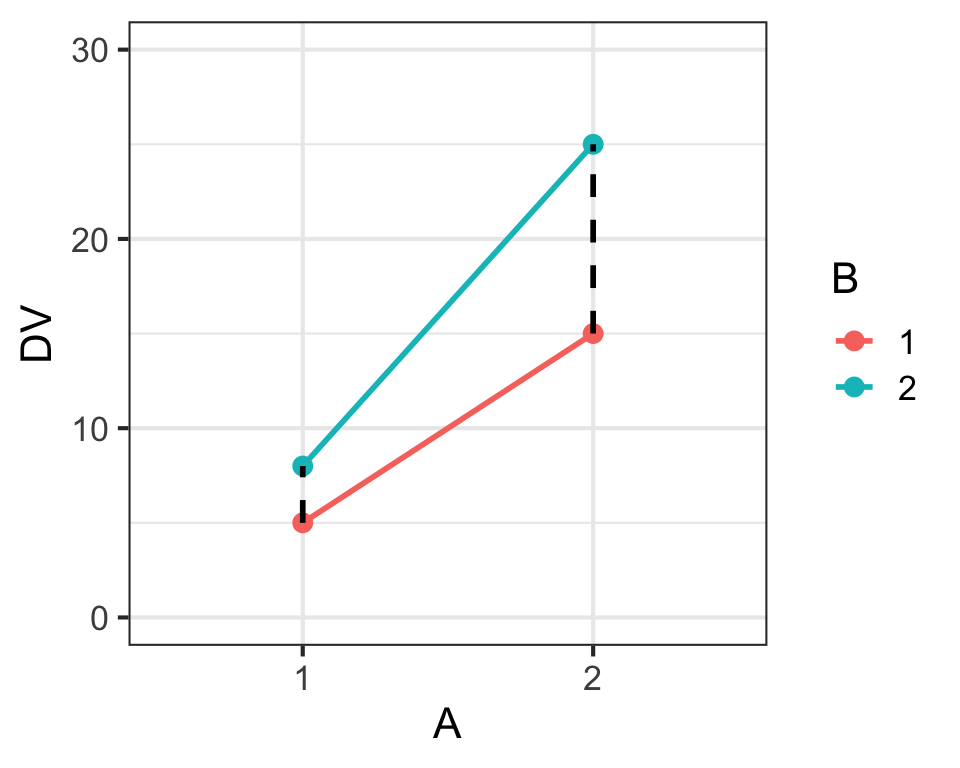
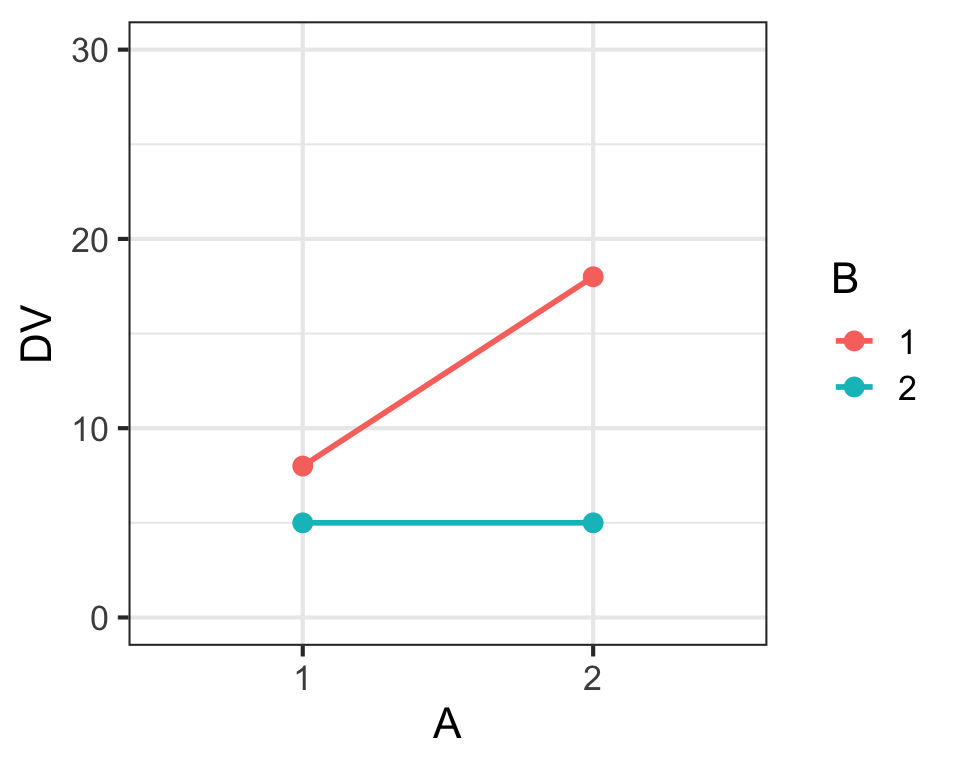
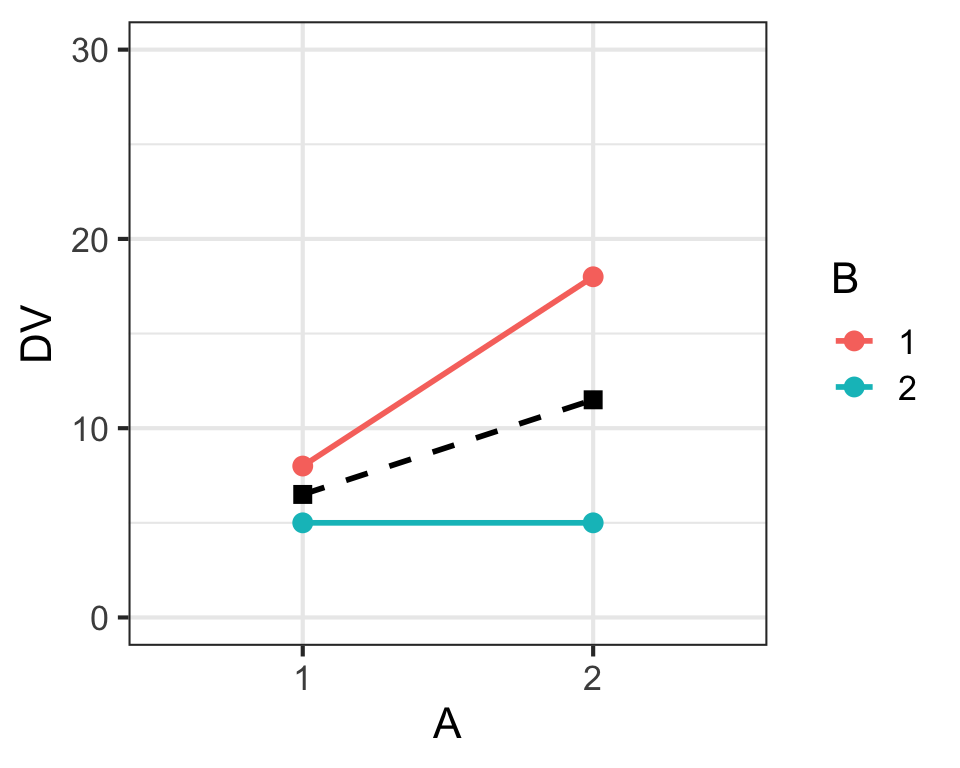
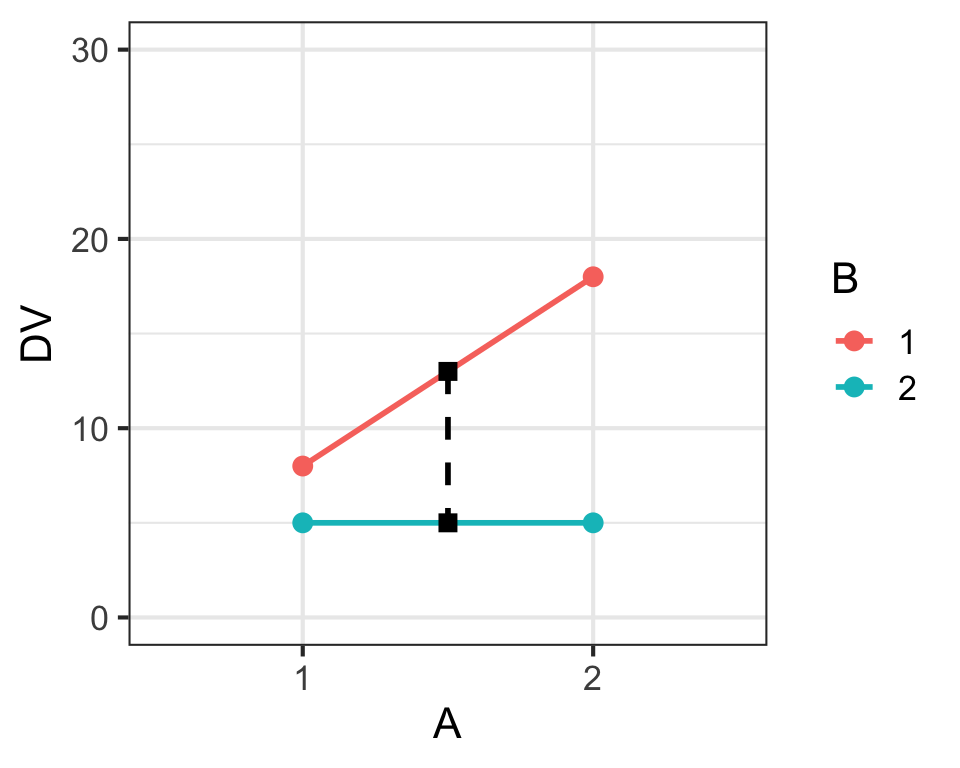
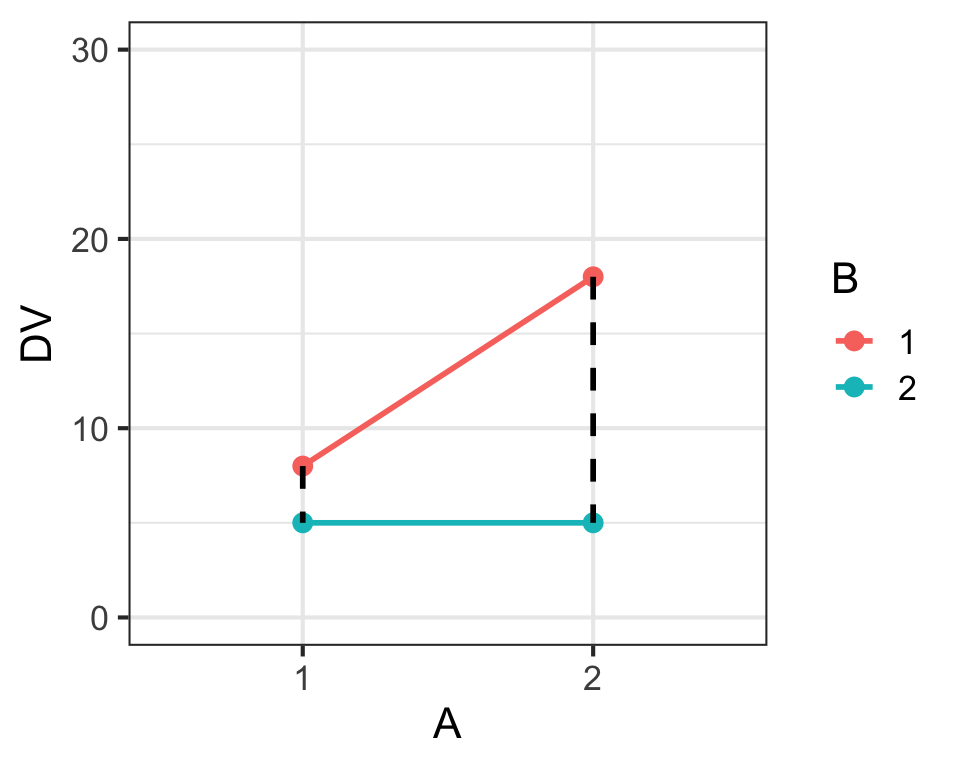
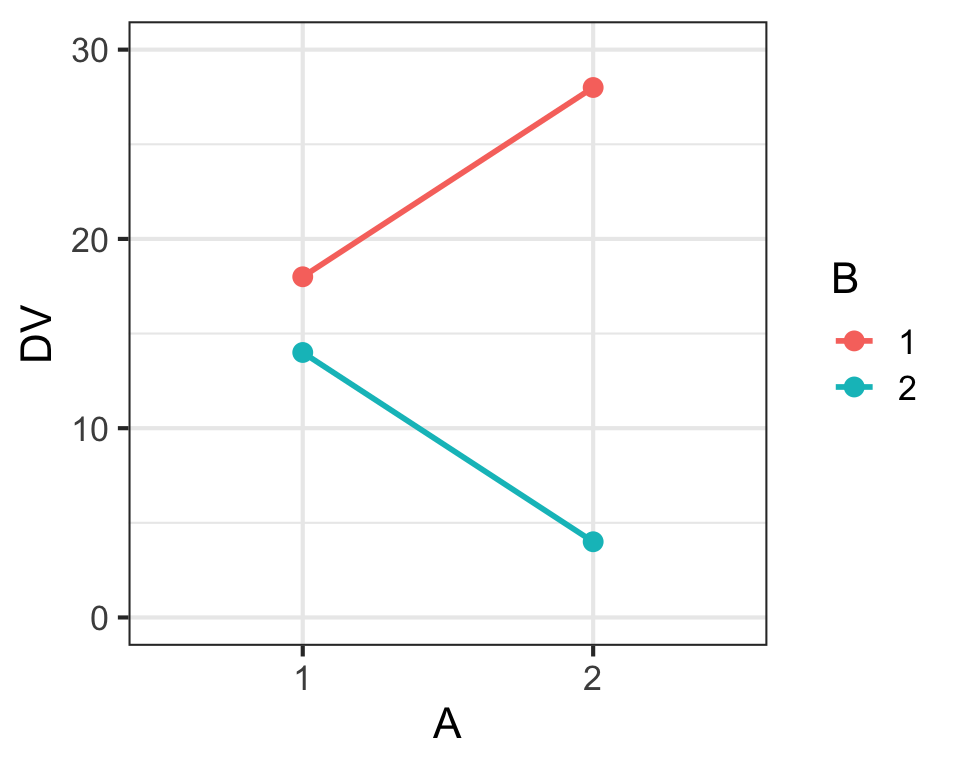
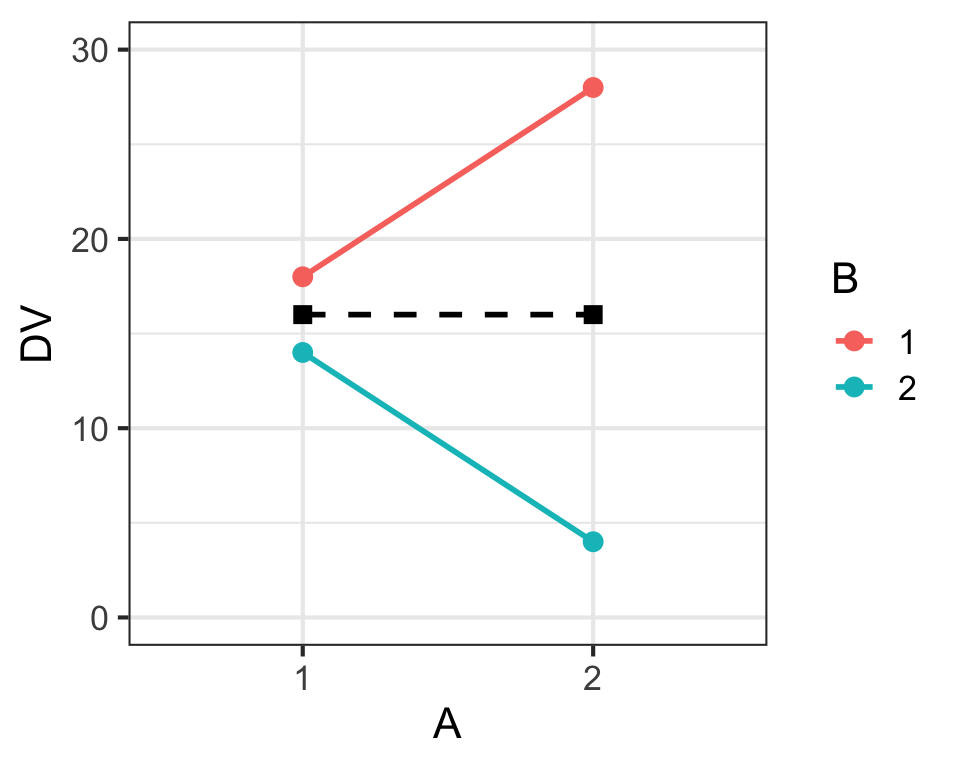
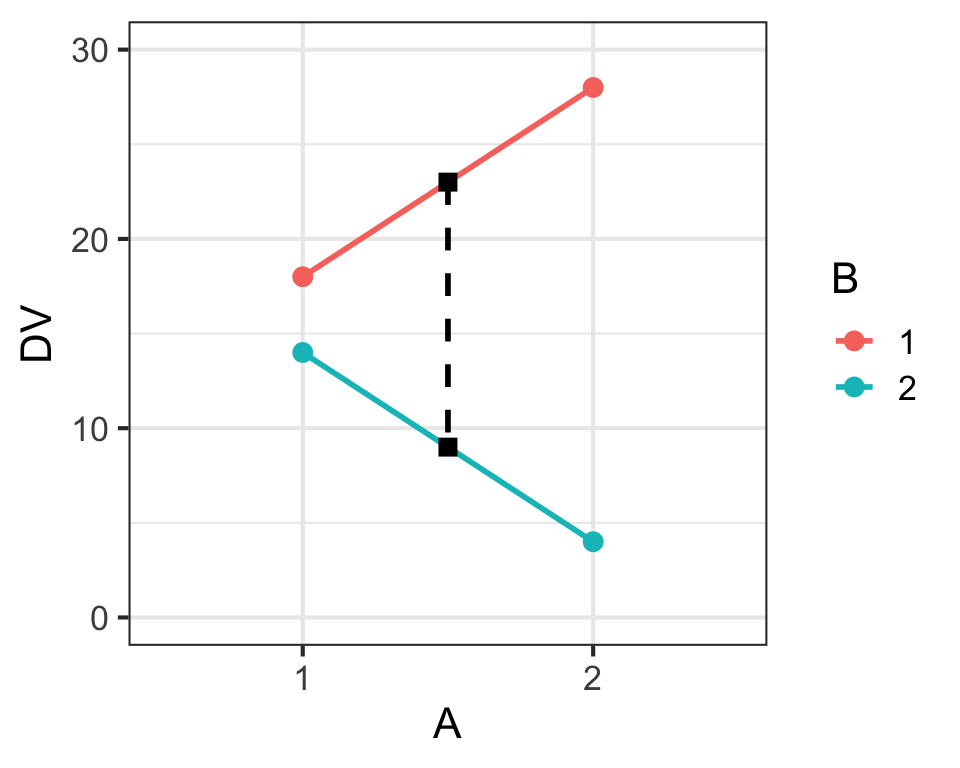
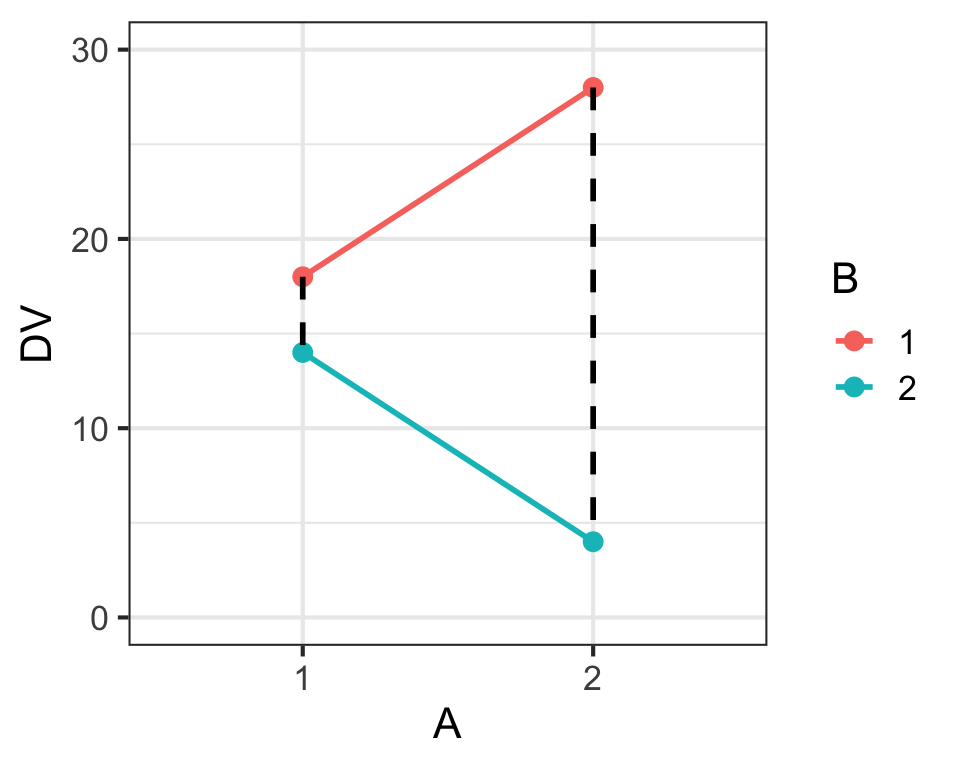
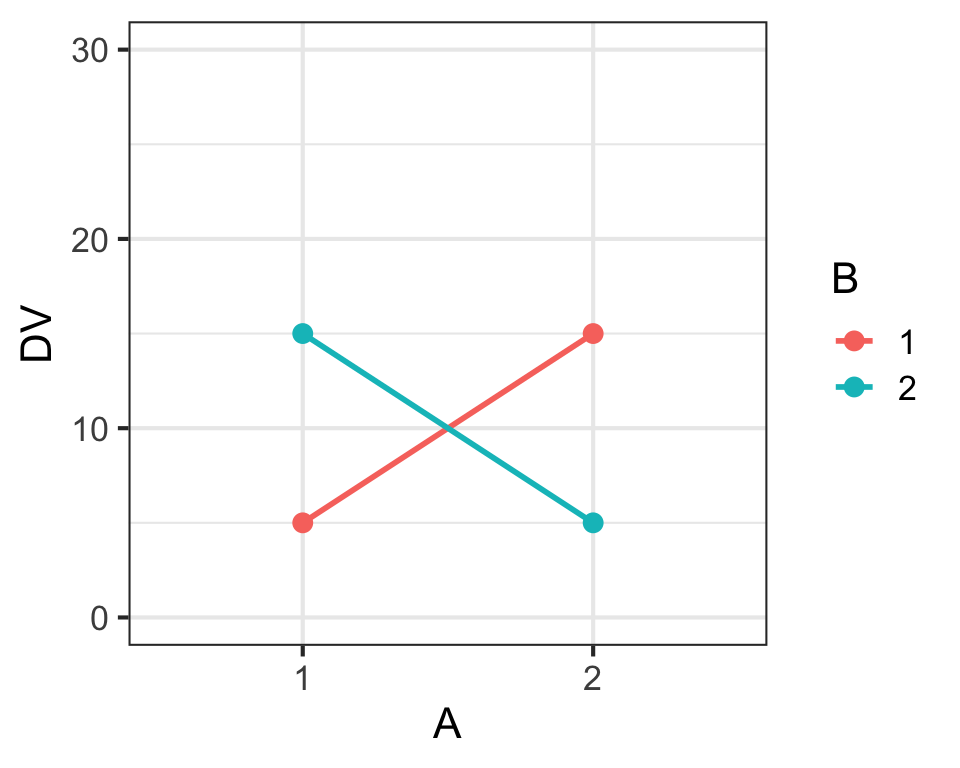
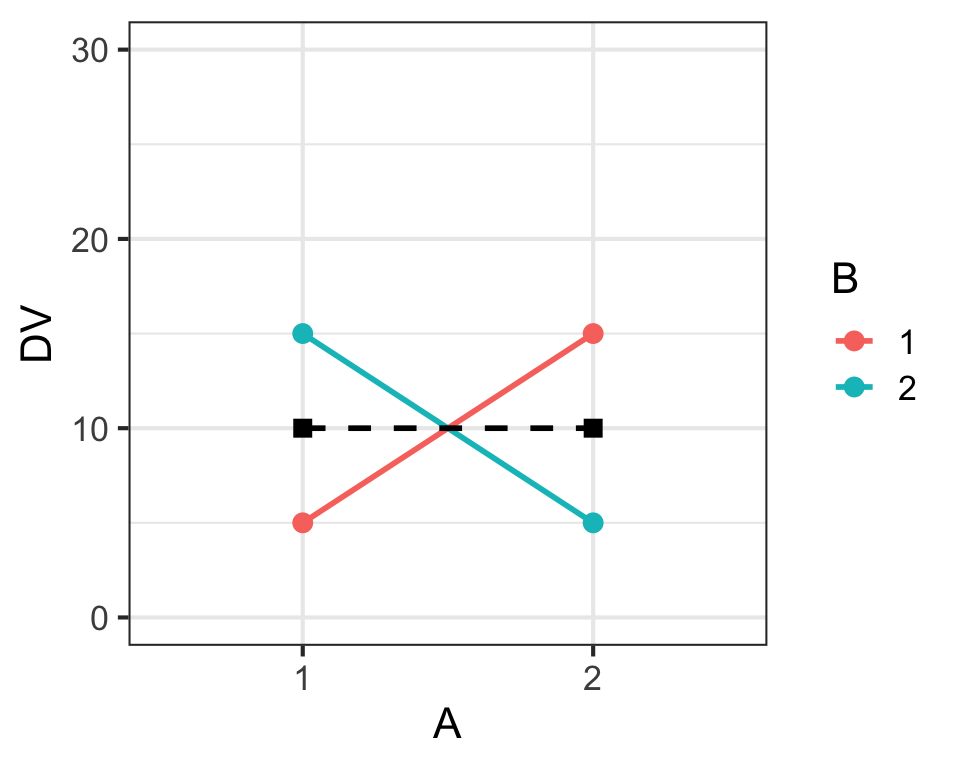
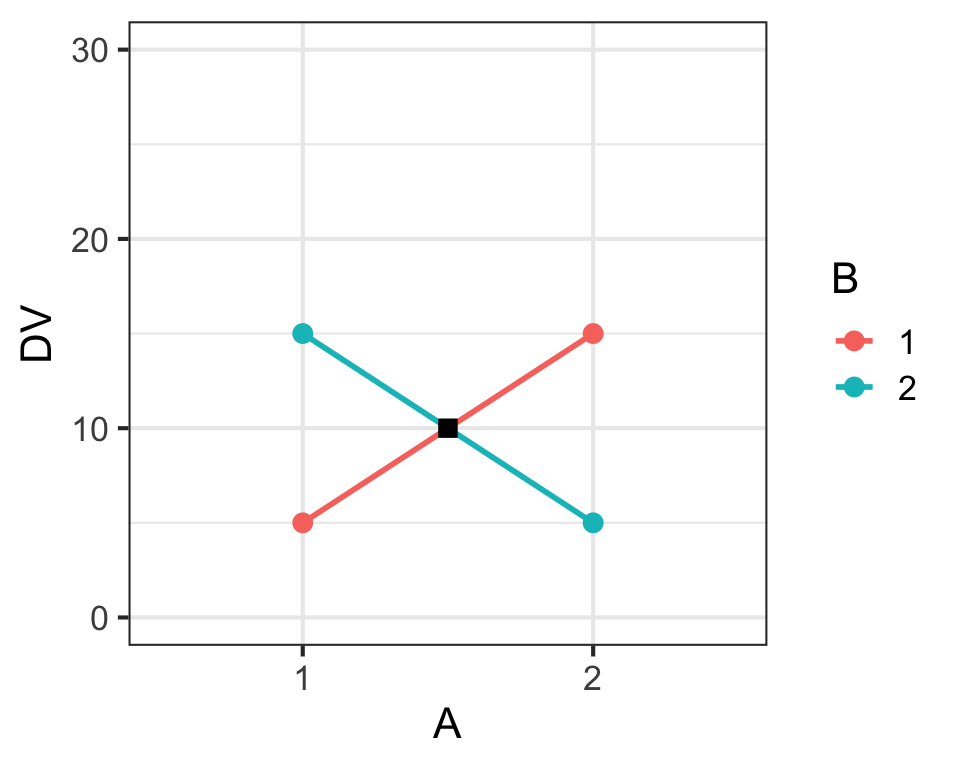
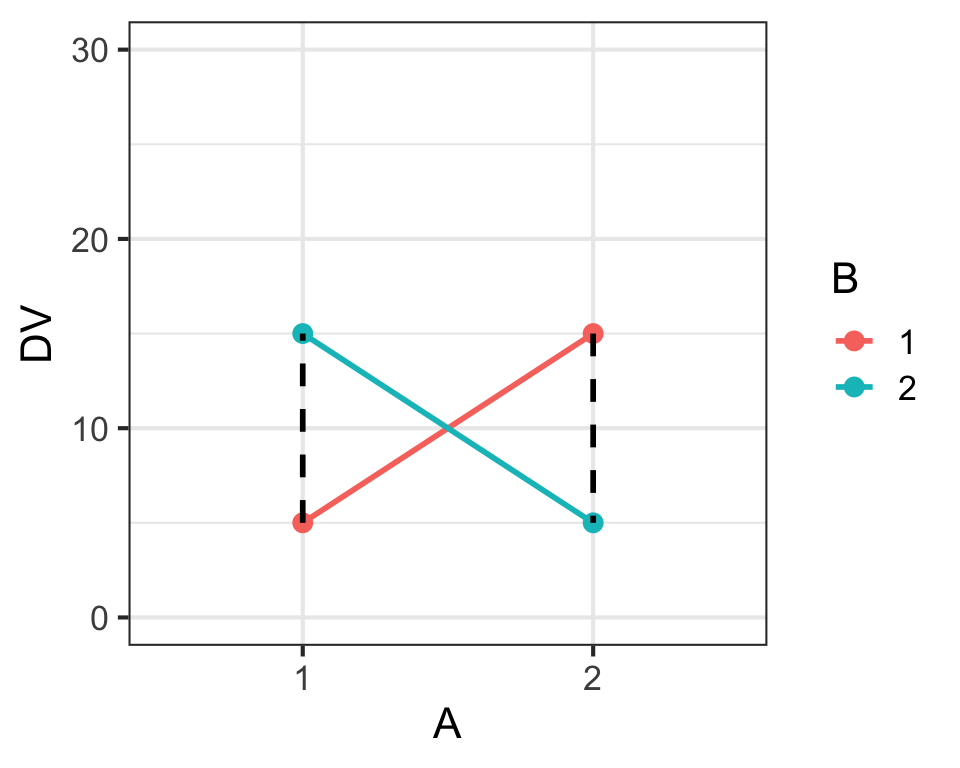
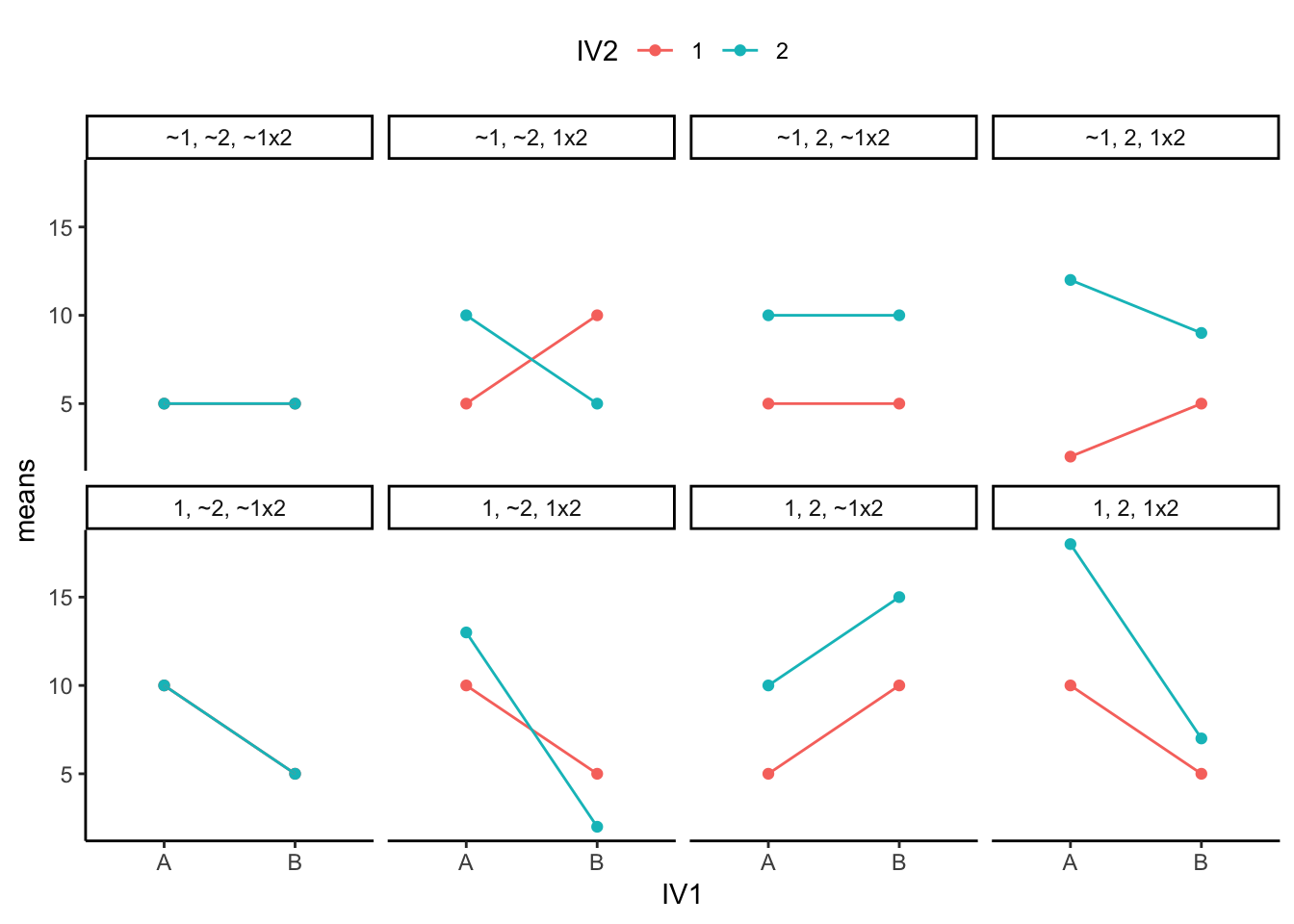
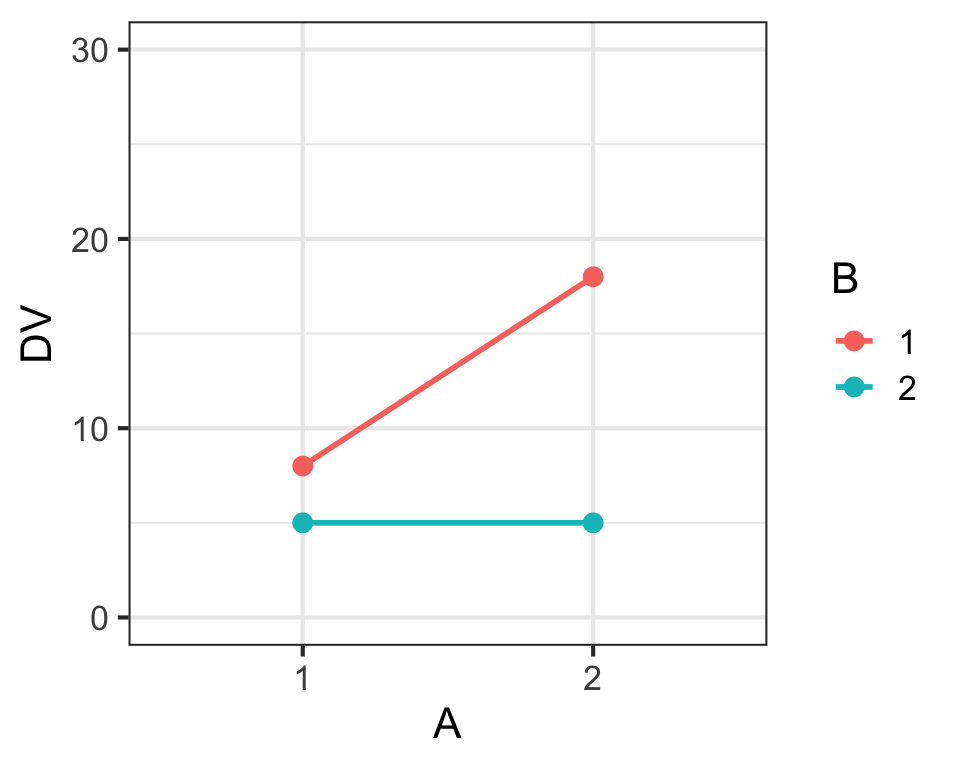
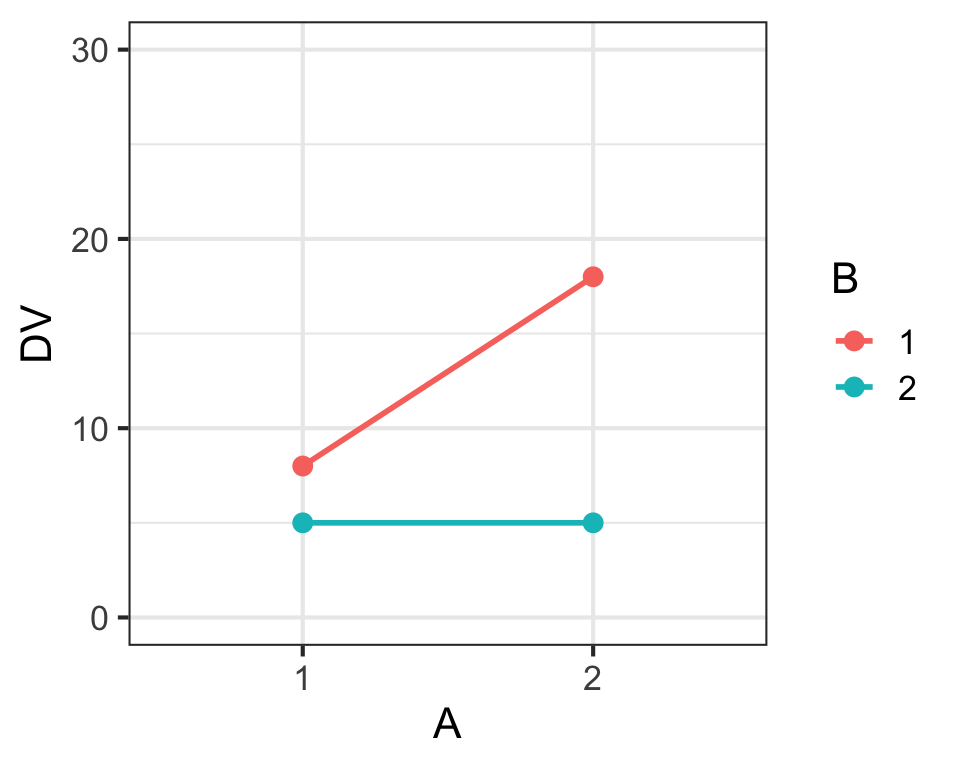
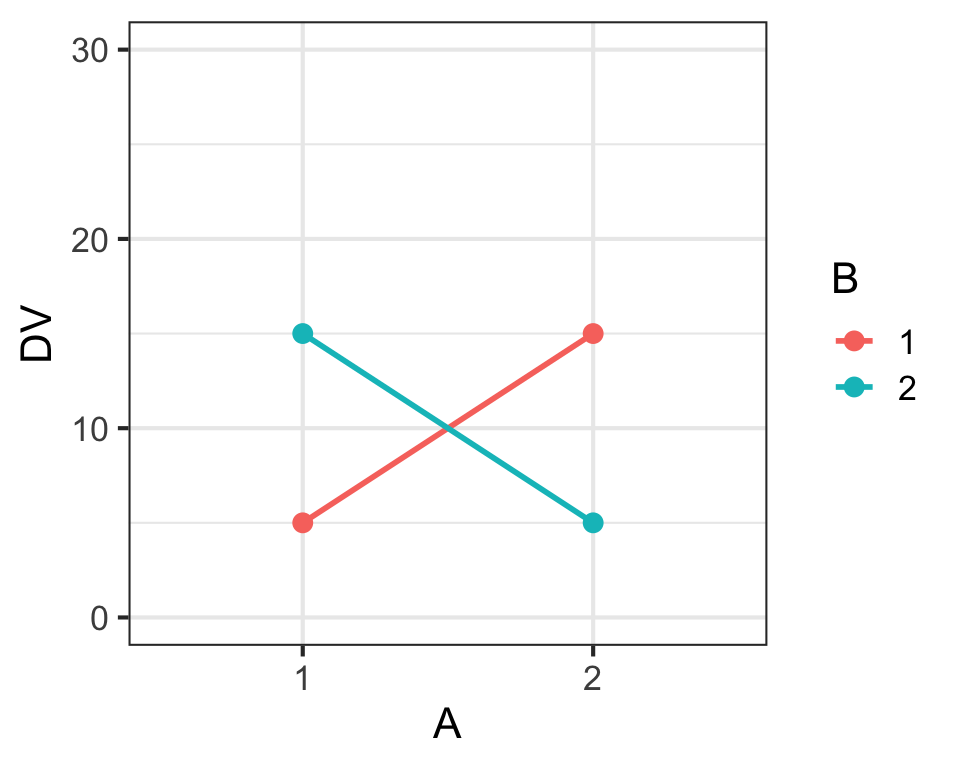
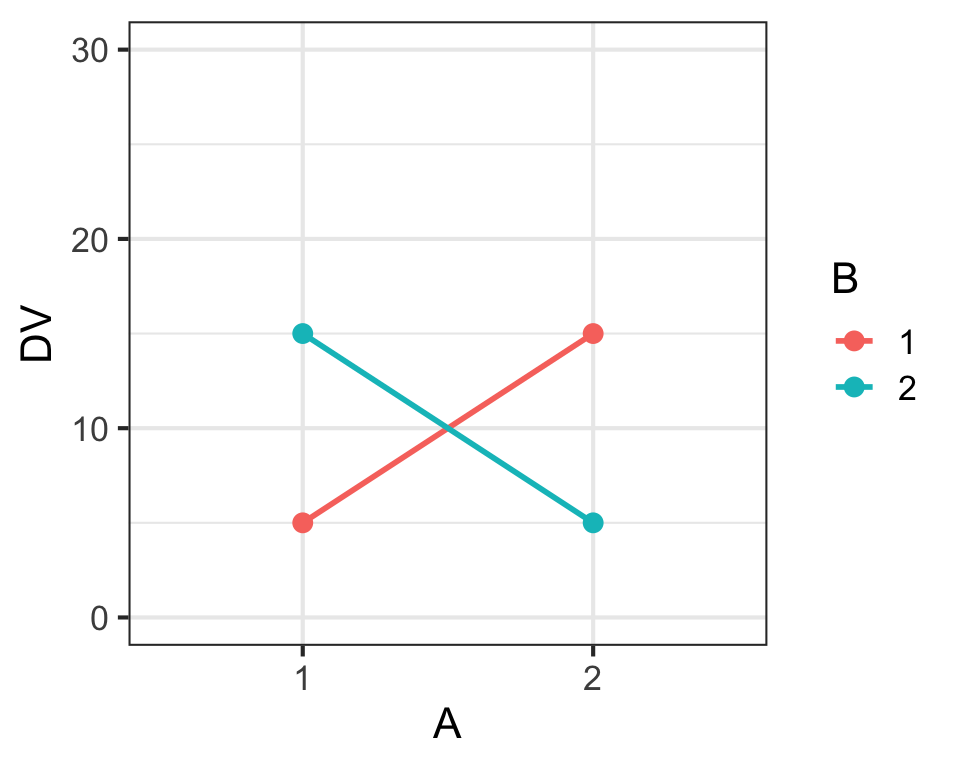
Main Effects & Interaction
- SSdrug + SSres = SStot
- 3.453 + 1.392 = 4.85
Df Sum Sq Mean Sq F value Pr(>F)
drug 2 3.453 1.7267 18.61 8.65e-05
Residuals 15 1.392 0.0928 - SStherapy + SSres = SStot
- 0.467 + 4.378 = 4.85
Df Sum Sq Mean Sq F value Pr(>F)
therapy 1 0.467 0.4672 1.708 0.21
Residuals 16 4.378 0.2736 - SSdrug + SStherapy + SSres = SStot
- 3.453 + 0.467 + 0.924 = 4.85
Df Sum Sq Mean Sq F value Pr(>F)
drug 2 3.453 1.7267 26.149 1.87e-05
therapy 1 0.467 0.4672 7.076 0.0187
Residuals 14 0.924 0.0660 - SSdrug + SStherapy + SSinteraction + SSres = SStot
- 3.453 + 0.467 + 0.271 + 0.653 = 4.85
Df Sum Sq Mean Sq F value Pr(>F)
drug 2 3.453 1.7267 31.714 1.62e-05
therapy 1 0.467 0.4672 8.582 0.0126
drug:therapy 2 0.271 0.1356 2.490 0.1246
Residuals 12 0.653 0.0544 - SSres is even smaller!
- reduces unexplained variance in the DV
- denominator of F-statistic is smaller
- F-statistics for our main effects are bigger
- p-values for our main effects are smaller