Logistic Regression
Week 5
The Donner Party
In 1846 the Donner and Reed families left Springfield, Illinois, for California by covered wagon. In July, the Donner Party, as it became known, reached Fort Bridger, Wyoming. There its leaders decided to attempt a new and untested rote to the Sacramento Valley. Having reached its full size of 89 people and 20 wagons, the party was delayed by a difficult crossing of the Wasatch Range and again in the crossing of the desert west of the Great Salt Lake. The group became stranded in the eastern Sierra Nevada mountains when the region was hit by heavy snows in late October. By the time the last survivor was rescued on April 21, 1847, 41 of the 89 members had died from famine and exposure to extreme cold.
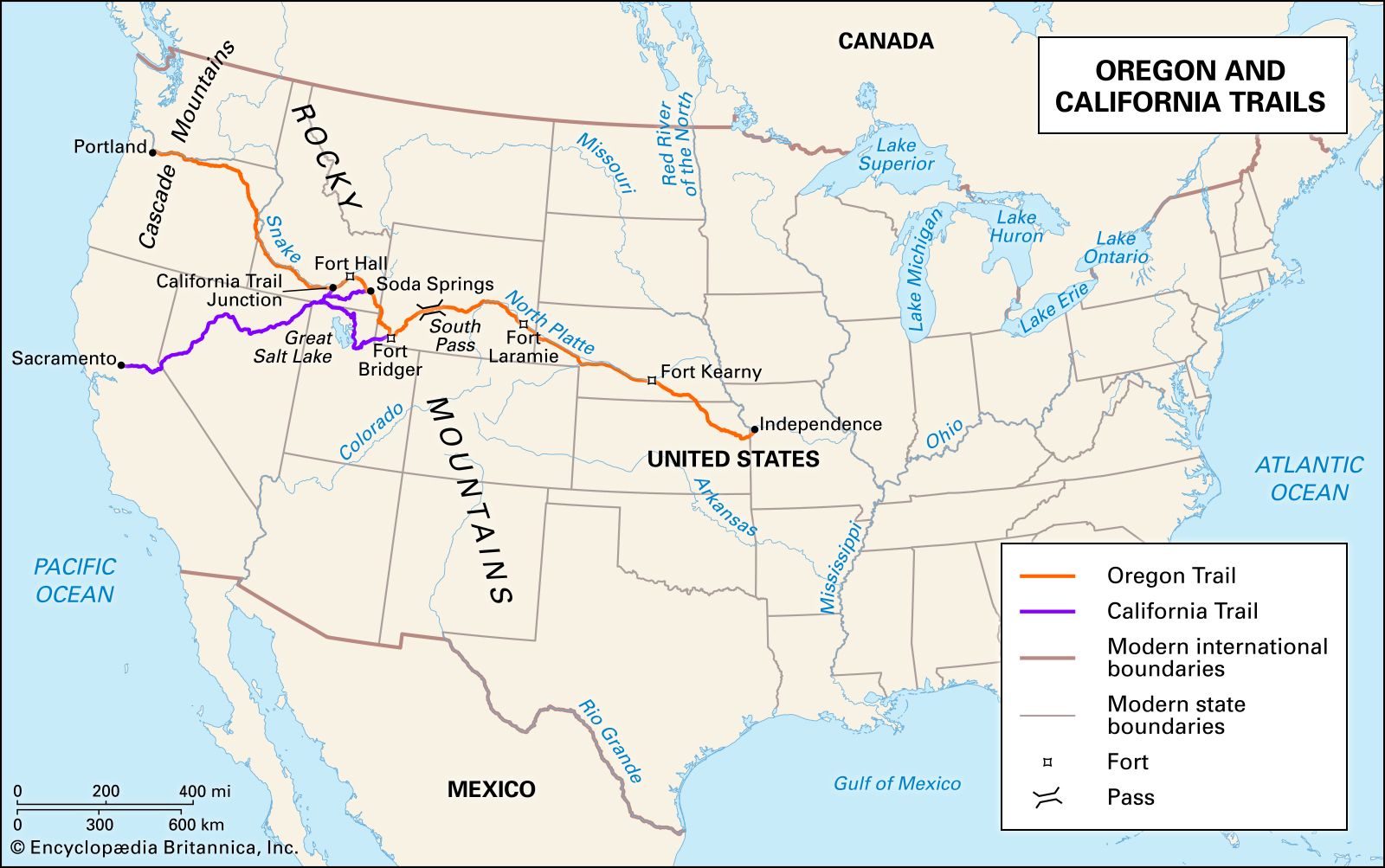

The Donner Party
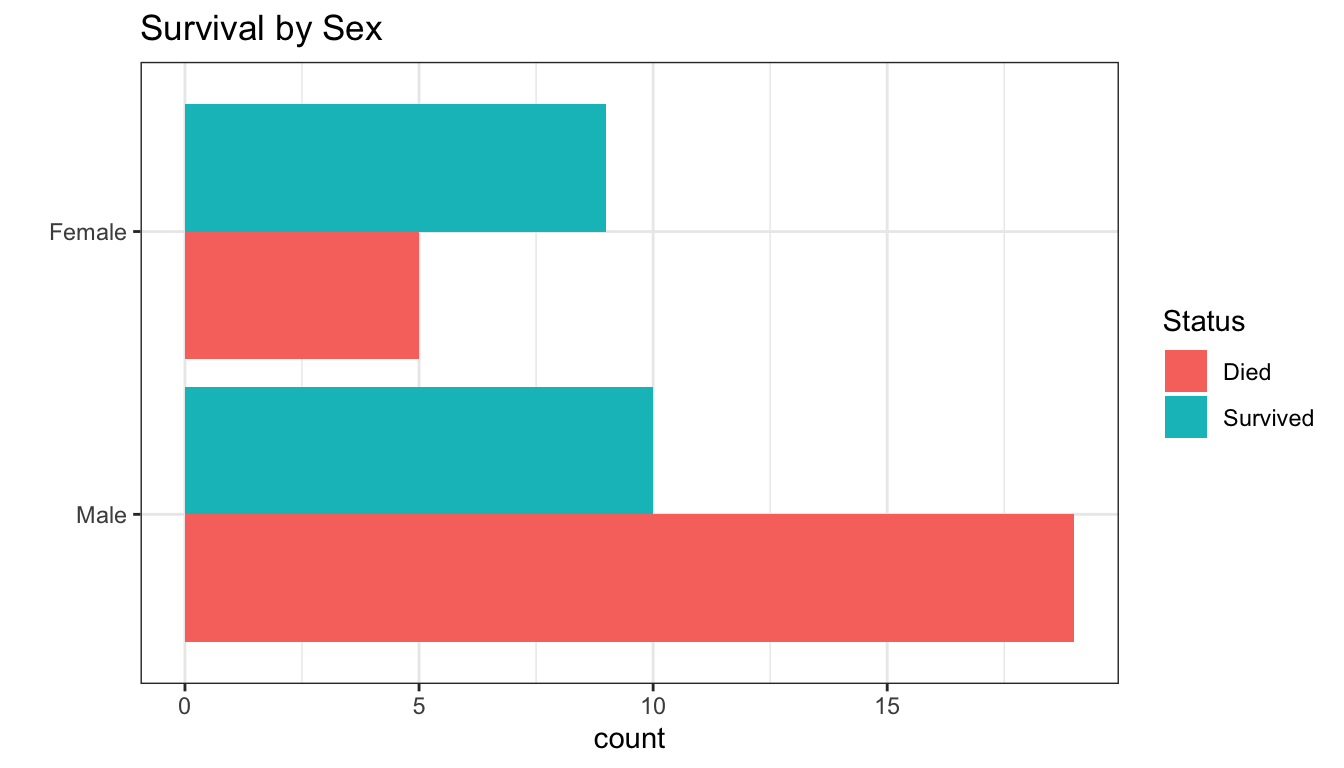
41 of the 89 members died
- what characteristics of those who died were different from those who survived?
- sex?
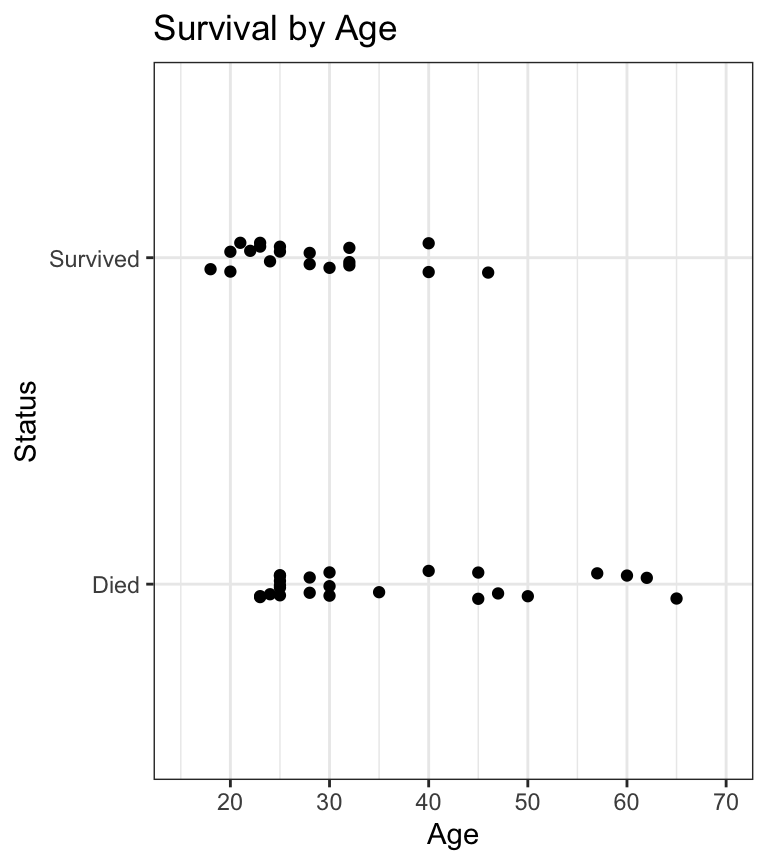
- age?
- can we build a model to predict who would survive based on these characteristics?
The Donner Party
# A tibble: 6 × 3
Age Sex Status
<dbl> <fct> <fct>
1 23 Male Died
2 40 Female Survived
3 40 Male Survived
4 30 Male Died
5 28 Male Died
6 40 Male Died Rows: 43
Columns: 3
$ Age <dbl> 23, 40, 40, 30, 28, 40, 45, 62, 65, 45, 25, 28, 28, 23, 22, 23,…
$ Sex <fct> Male, Female, Male, Male, Male, Male, Female, Male, Male, Femal…
$ Status <fct> Died, Survived, Survived, Died, Died, Died, Died, Died, Died, D…- data for “adults”, i.e. people who were over 15 years old
The Donner Party
The Donner Party
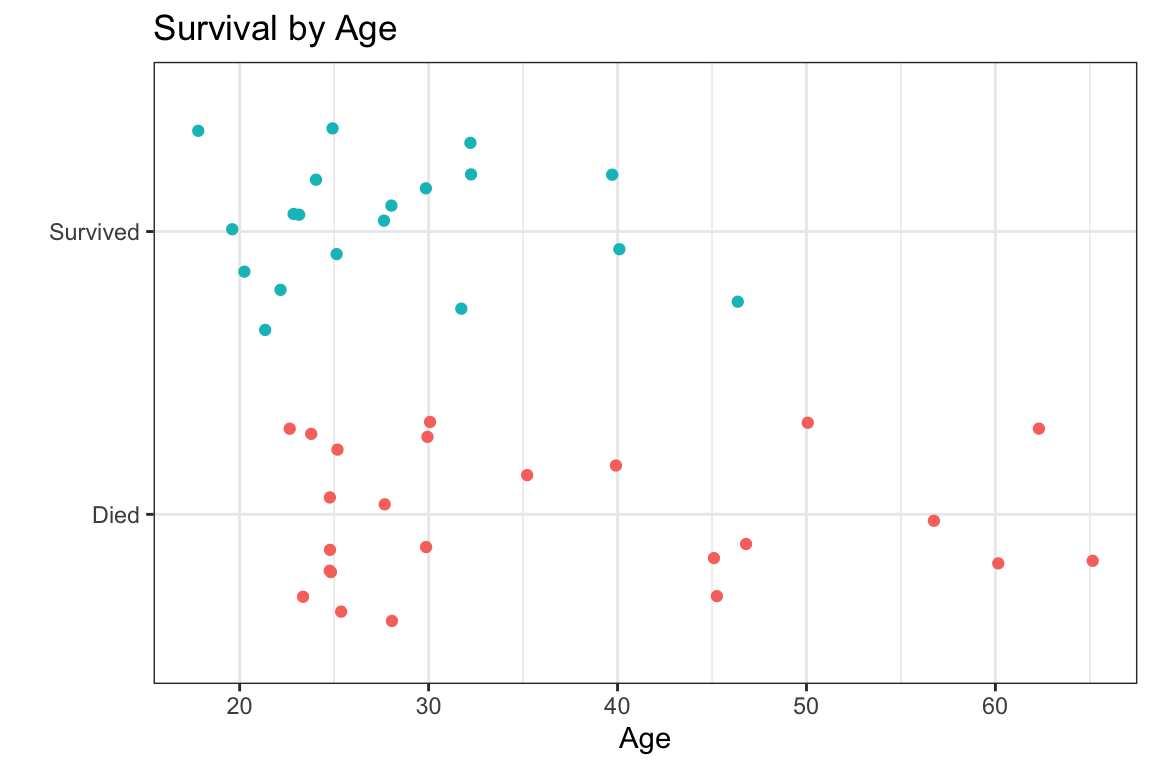
The Donner Party
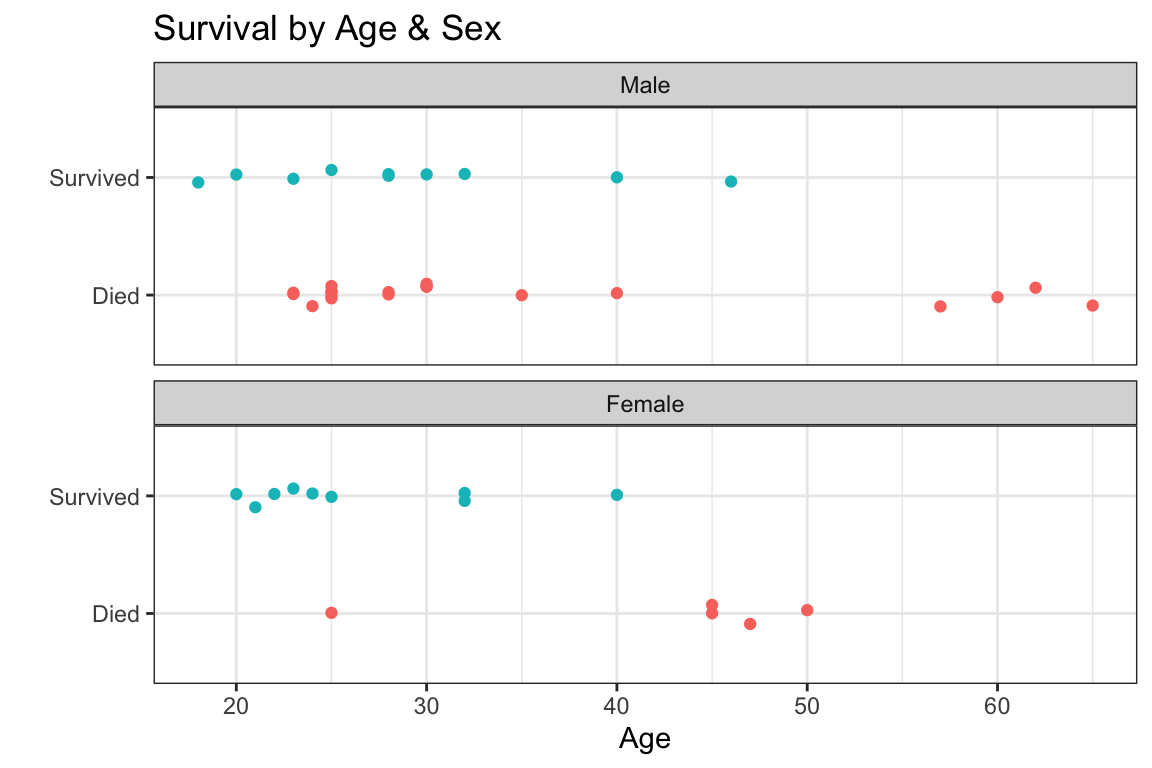
The Donner Party
- what’s the probability of survival given age?
- logistic regression models the probability of a binary outcome as a function of one or more predictors
- e.g. probability of
Status(binary outcome:SurvivedvsDied) as a function ofAge(continuous variable)
The Donner Party
Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
ggplot(aes(x=Age, y=prob, color=Sex)) +
geom_jitter(height=0.025, width=0) +
lims(x=c(15,70), y=c(-0.1,1.1)) +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="glm", method.args=list(family="binomial"), se=FALSE, fullrange=TRUE) +
labs(title="Donner party", y="Probability of Survival") +
theme_bw()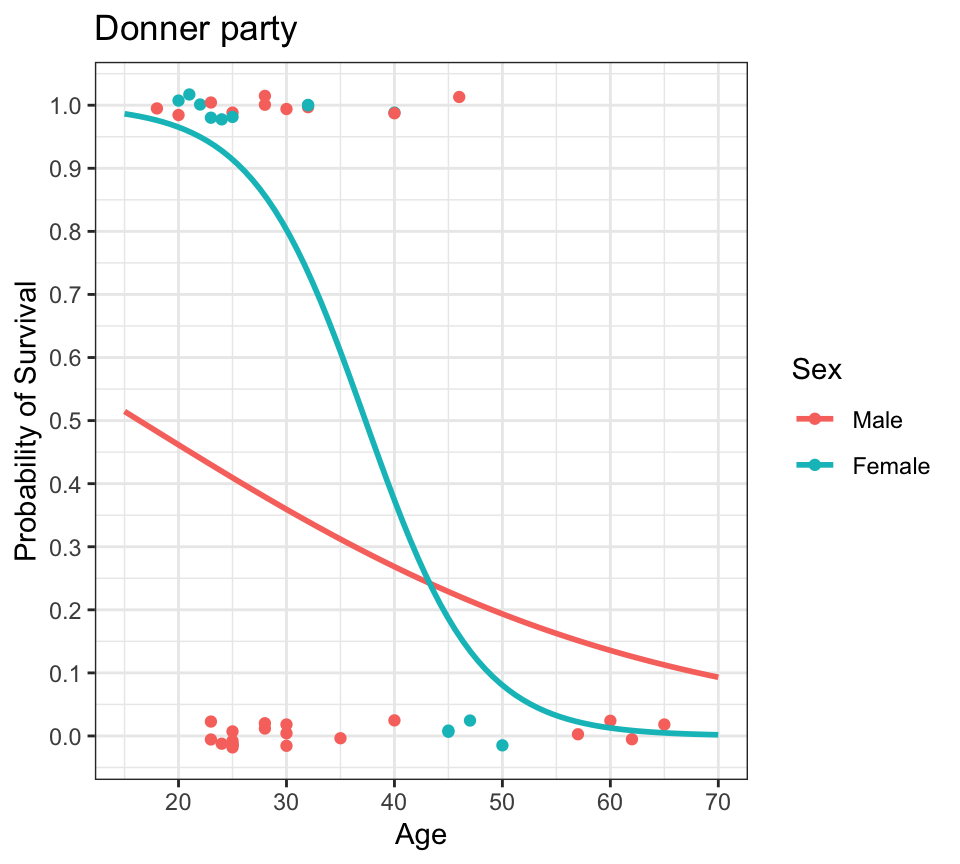
- what’s the probability of survival as a function of age, by sex?
- we can plot a logistic regression fit in
ggploteasily usinggeom_smooth() - logistic regression lines are usually S-shaped (sigmoidal)
Logistic Regression
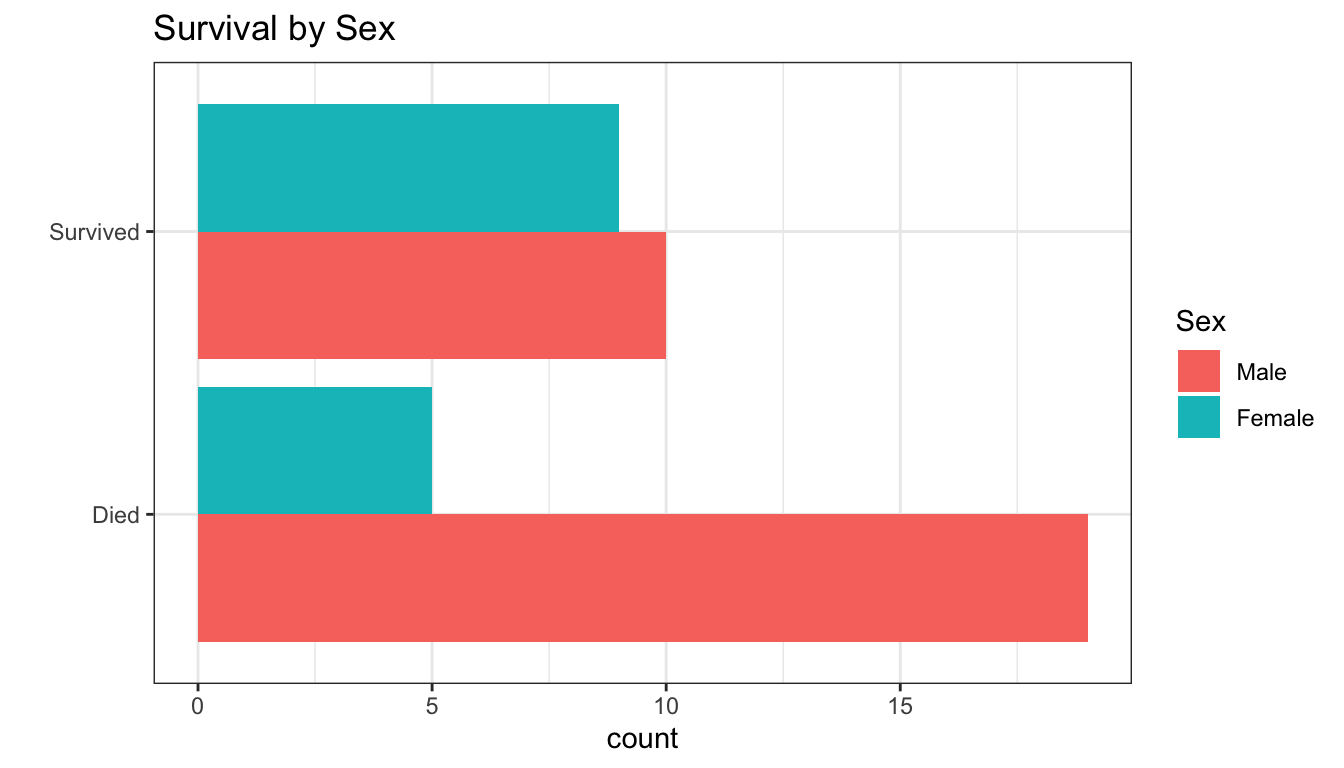
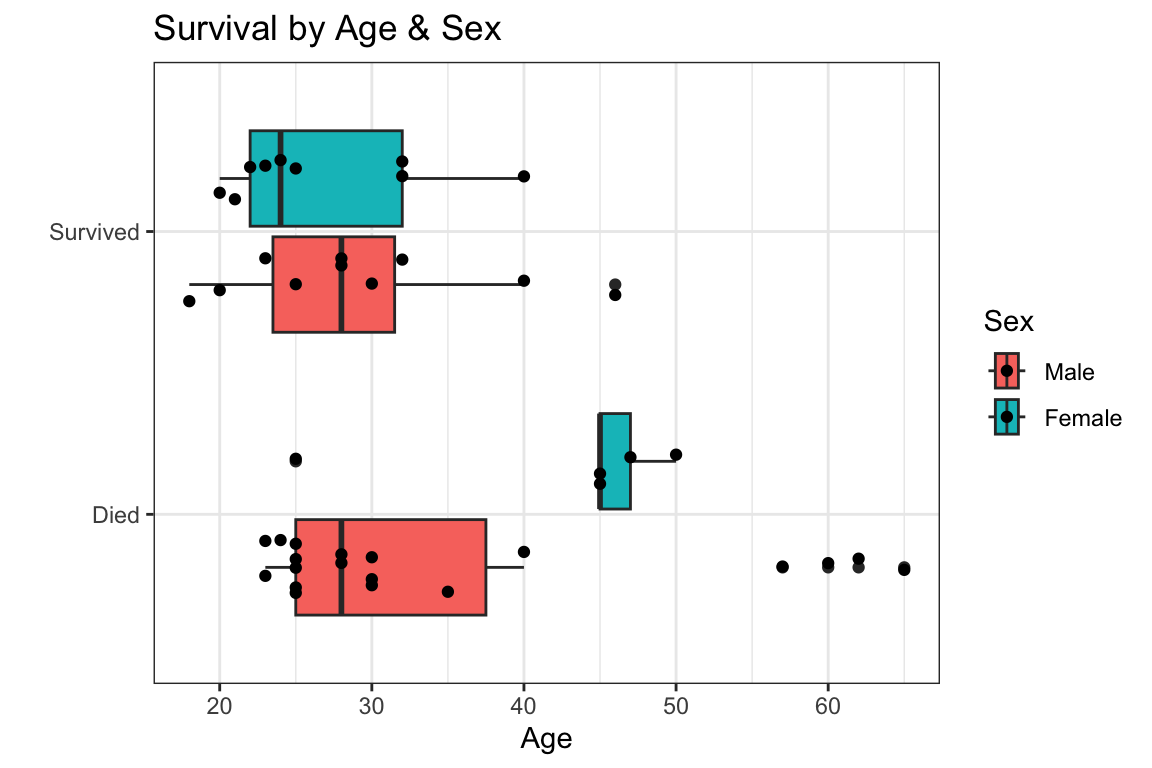
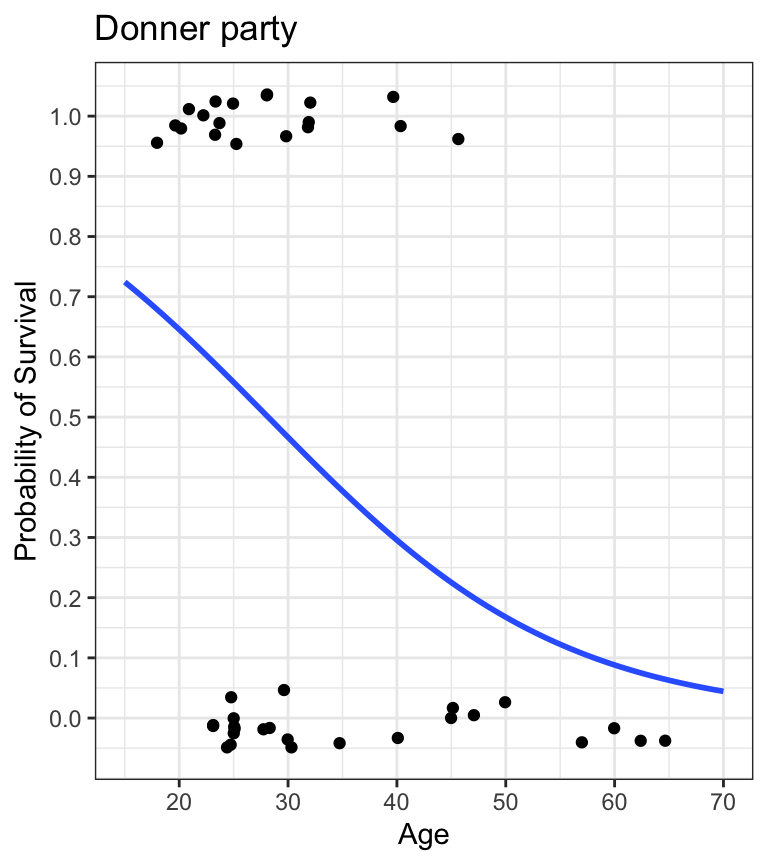
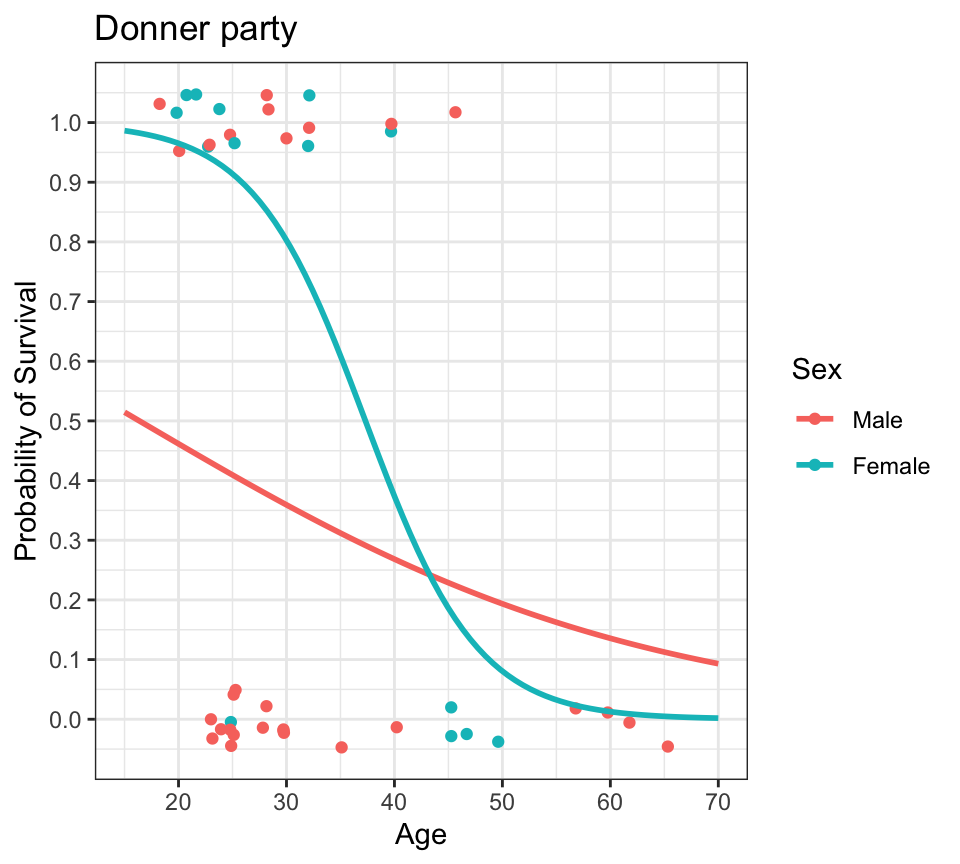
- these are all descriptive ways of looking at the relationship between characteristics (age, sex) and probability of survival
- logistic regression can give us a quantitative way of describing these relationships
Logistic Regression
- we can also use logistic regression to predict outcomes for new observations
- e.g. predict 5-year survival of breast cancer patients based on tumour size, lymph node involvement, and tumour grade
- e.g. predict mortgage default based on income, credit score, and debt-to-income ratio
- when the dependent variable is binary, we use logistic regression
- dependent variable is binary
- independent variables can be continuous (e.g. Age) or categorical (e.g. Sex)
Why not linear regression?
- why do we need logistic regression?
- why not just use linear regression?
- let’s try it and see what happens
Why not linear regression?
Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
filter(Sex=="Female") %>%
ggplot(aes(x=Age, y=prob)) +
geom_jitter(height=0.05, width=0, color="black") +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="lm", se=FALSE, fullrange=TRUE, color="orange") +
lims(x=c(0,80), y=c(-0.5,1.5)) +
labs(title="Donner party (Females)", y="Probability of Survival") +
theme_bw()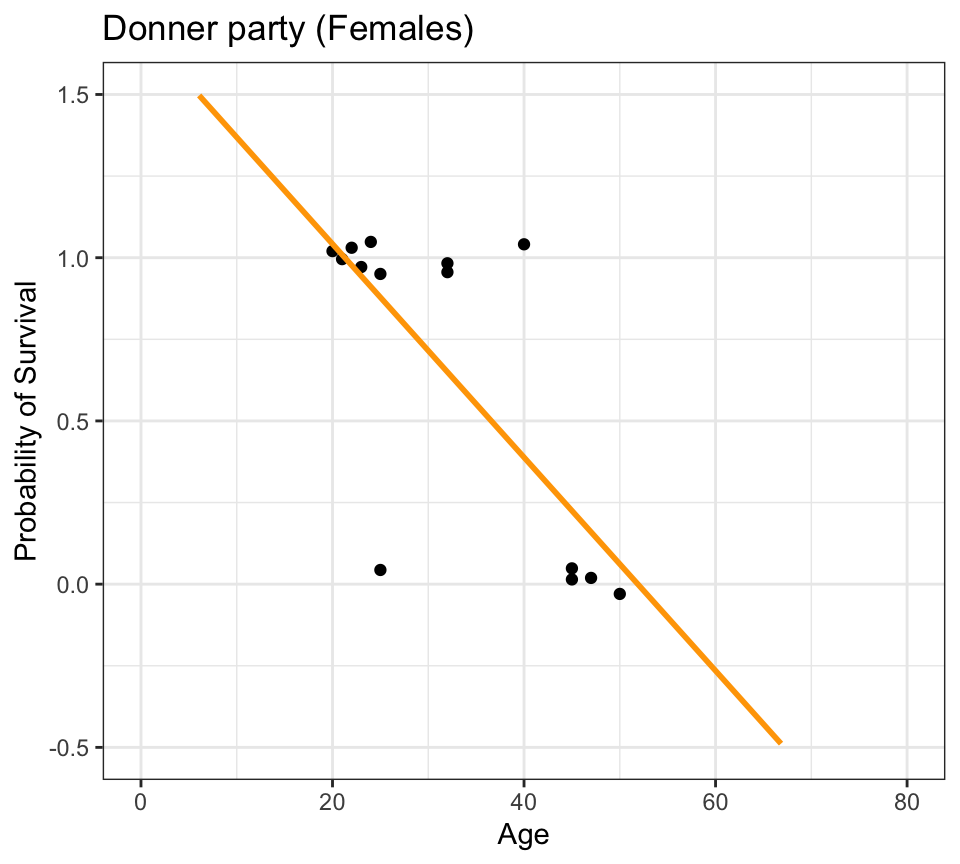
- linear regression model prediction extends above 1.0 and below 0.0
- doesn’t make any sense given the thing we’re trying to model is a probability
- probabilities can only live between 0.0 and 1.0
Why not linear regression?
Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
filter(Sex=="Female") %>%
ggplot(aes(x=Age, y=prob)) +
geom_jitter(height=0.05, width=0) +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="lm", se=FALSE, fullrange=TRUE, color="orange") +
geom_smooth(method="glm", method.args=list(family="binomial"), se=FALSE, fullrange=TRUE, color="blue") +
lims(x=c(5,70), y=c(-0.5,1.5)) +
labs(title="Donner party (Females)", y="Probability of Survival") +
theme_bw()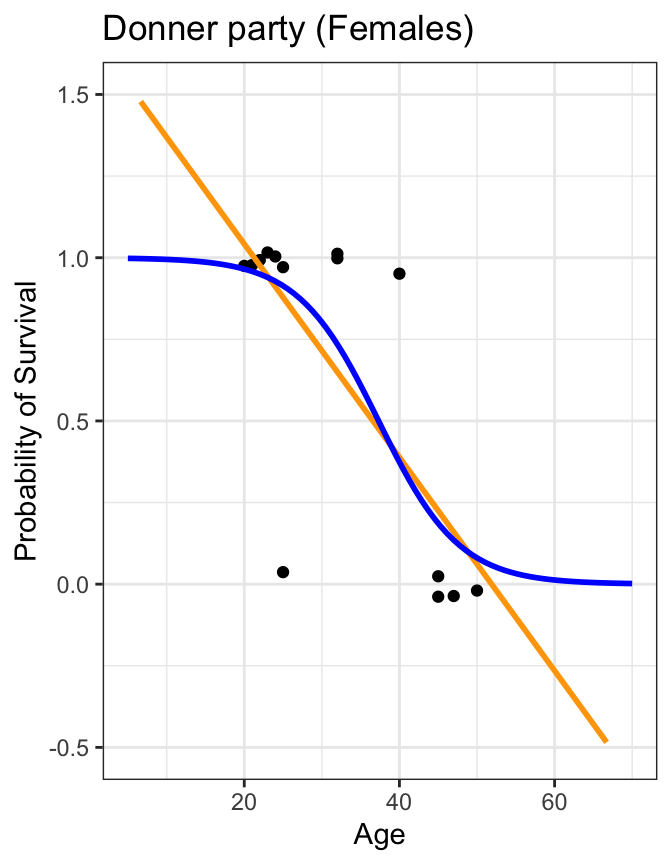
Also: we violate assumptions of linear regression
- linearity: relationship between predictor and outcome is not linear
- normality: residuals are not normally distributed
- homoscedasticity: variance of residuals is not constant over the range of the predictor variable
Logistic Regression
Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
filter(Sex=="Female") %>%
ggplot(aes(x=Age, y=prob)) +
geom_jitter(height=0.05, width=0) +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="glm", method.args=list(family="binomial"), se=FALSE, fullrange=TRUE, color="blue") +
lims(x=c(5,70), y=c(-0.05,1.05)) +
labs(title="Donner party (Females)", y="Probability of Survival") +
theme_bw()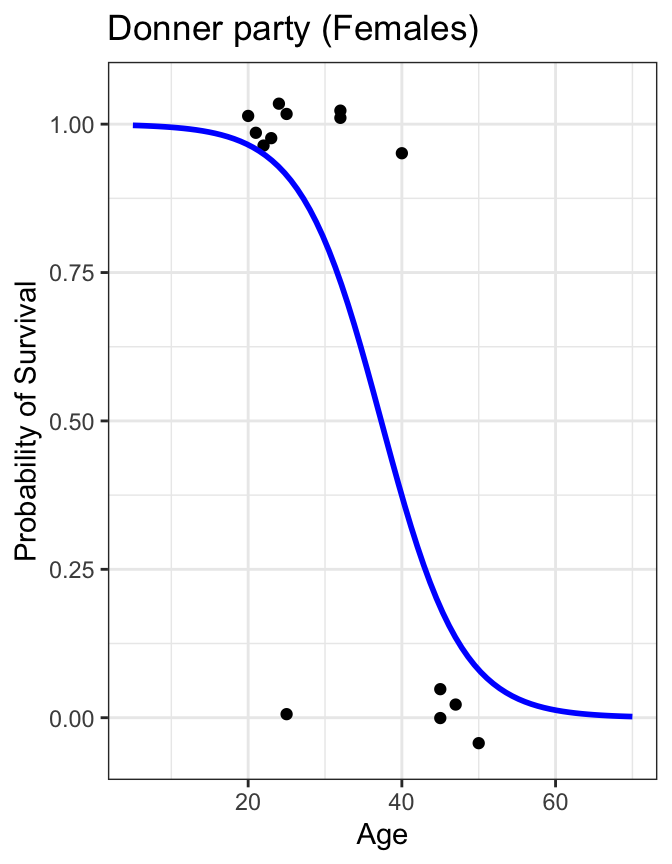
- we can treat Survived and Died as successes and failures arising from a binomial distribution where the probability of a success is given by a transformation of a linear model of the predictor(s)
- this is a general way of addressing this type of problem in regression, and the resulting models are called generalized linear models (GLMs)
- Logistic regression is just one example of a GLM
- but first: a reminder of the binomial distribution
Binomial Distribution
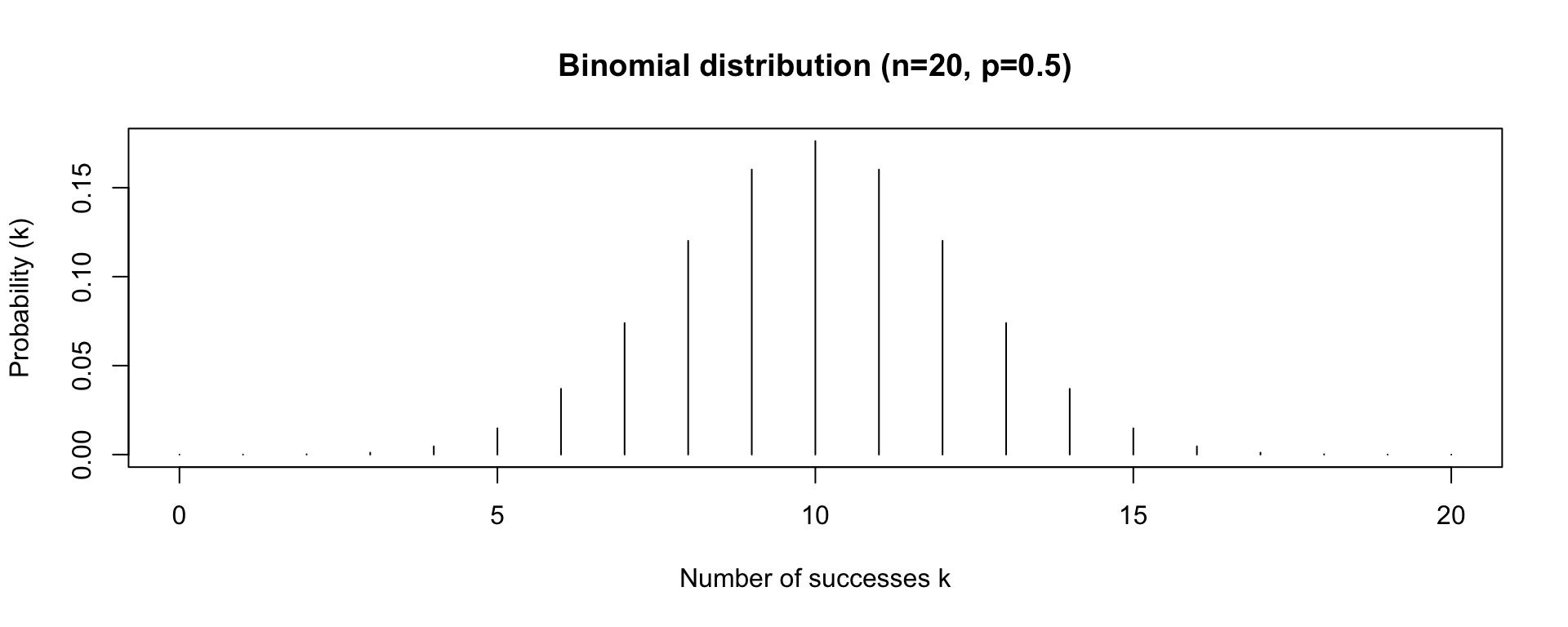
- the Binomial distribution has two parameters: n the number of trials, and p the probability of success on a given trial
- the Binomial distribution gives us the probability of observing k successes in n trials, given p
- e.g. probability of observing 3 heads in 20 coin flips, given that the probability of heads is 0.5
Binomial Distribution
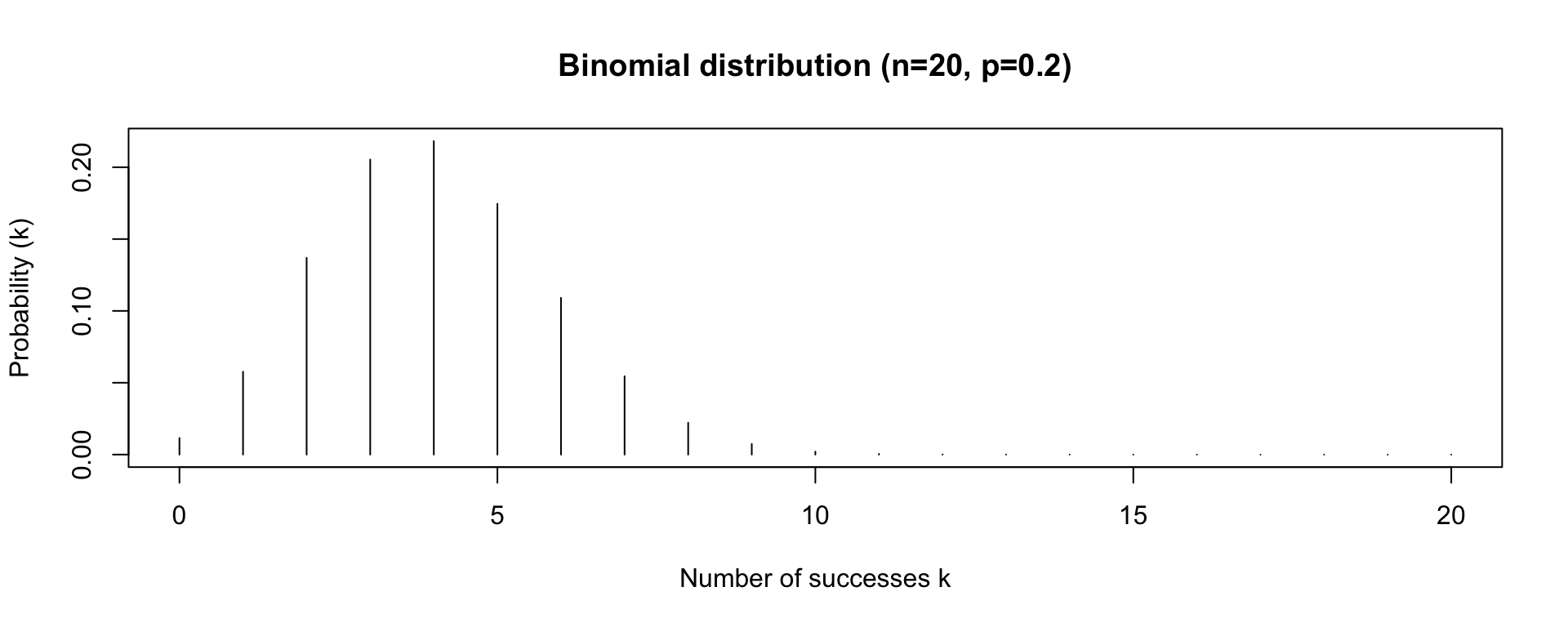
- the Binomial distribution has two parameters: n the number of trials, and p the probability of success on a given trial
- the Binomial distribution gives us the probability of observing k successes in n trials, given p
- e.g. probability of observing 3 heads in 20 coin flips, given that the probability of heads is 0.2
Generalized Linear Models (GLMs)
All GLMs have four components:
- an outcome variable that is being predicted and predictor variables to predict the outcome
- a probability distribution describing the outcome variable
- a linear model \eta = \beta_{0} + \beta_{1}X_{1} + \dots + \beta_{n}X_{n} where \eta is the linear predictor and X_{1}, \dots, X_{n} are the predictor variable(s)
- a link function relates the linear model to the parameter of the outcome variable:
g(p) = \eta
or
p = g^{-1}(\eta)
Logistic Regression
a GLM with a binomial distribution and a logit link function
- the outcome variable is binary (e.g. Survived or Died) and the predictor variable is continuous (e.g. Age)
- p (the probability of a success, e.g. Survival) is the parameter of the binomial distribution
Logistic Regression
a GLM with a binomial distribution and a logit link function
- the linear model of our predictor variable is: \eta = \beta_{0} + \beta_{1}\mathrm{Age}
- the link function is: logit(p) = log\left(\frac{p}{1-p}\right) = \eta
putting it together:
log\left(\frac{p}{1-p}\right) = \beta_{0} + \beta_{1}\mathrm{Age}
Properties of the Logit Function
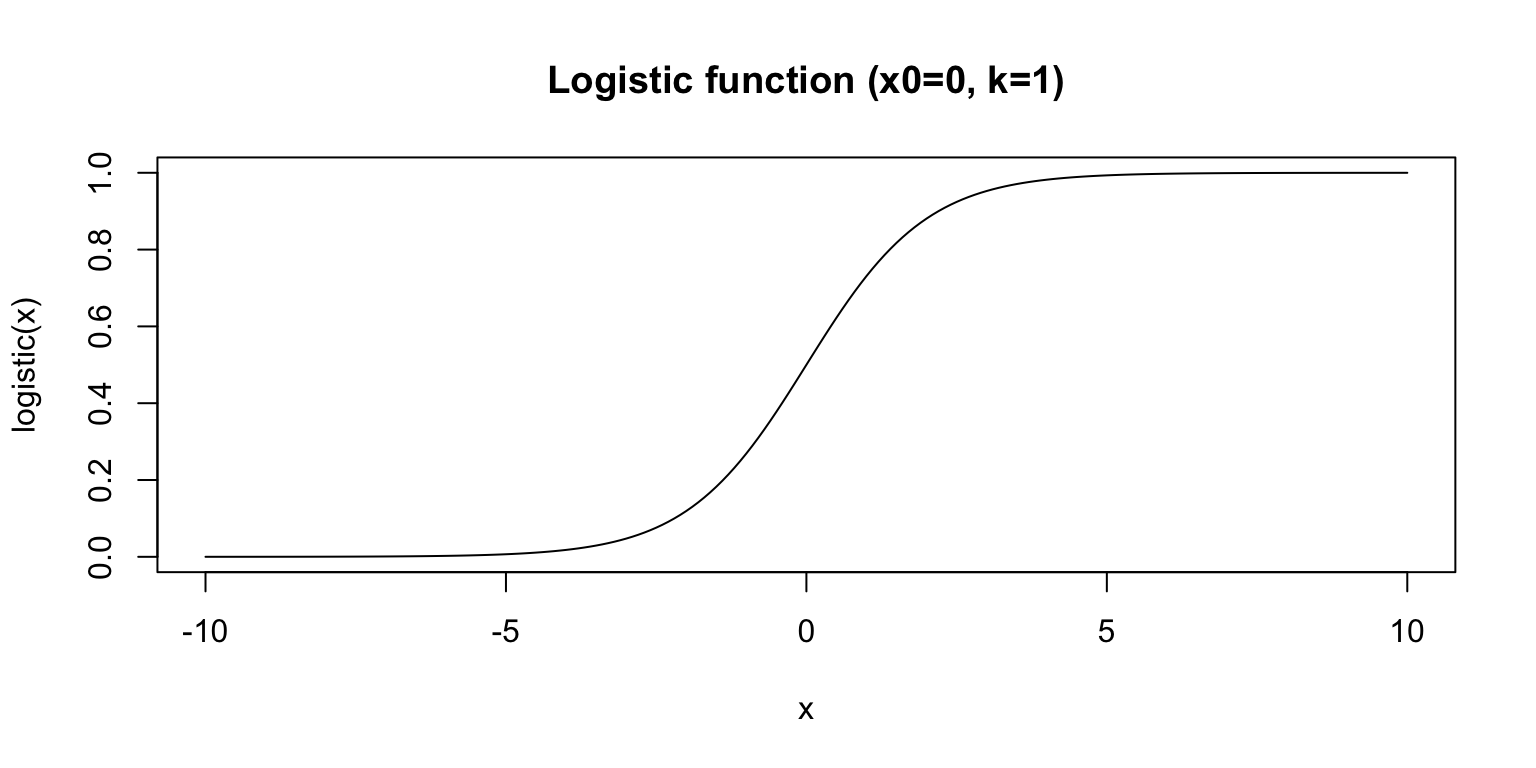
- the Logit function is the inverse of the Logistic function
- the Logistic function is an S-shaped curve that maps continuous values (-\infty to \infty) to the interval (0,1)
Logistic Regression
- log\left(\frac{p}{1-p}\right) = \beta_{0} + \beta_{1}\mathrm{Age}
- we can solve for p: p = \frac{e^{(\beta_{0} + \beta_{1}\mathrm{Age})}}{1 + e^{(\beta_{0} + \beta_{1}\mathrm{Age})}}
- this is the logistic regression model for the probability of survival as a function of age
Logistic Regression
p = \frac{e^{(\beta_{0} + \beta_{1}\mathrm{Age})}}{1 + e^{(\beta_{0} + \beta_{1}\mathrm{Age})}}
- we can estimate the parameters \beta_{0} and \beta_{1} from the data
- then we can plug in any value of Age to get a predicted probability of survival
- we can use this model to predict the probability of survival for any age
- e.g. what’s the probability of survival for a 30-year-old?
p = \frac{e^{\beta_{0} + \beta_{1}\mathrm{Age}}}{1 + e^{\beta_{0} + \beta_{1}\mathrm{Age}}} = \frac{e^{\beta_{0} + \beta_{1}(30)}}{1 + e^{\beta_{0} + \beta_{1}(30)}}
Logistic Regression in R
- we can fit a logistic regression model in R using the
glm()function glm()is a general function for fitting generalized linear models- for logistic regression, the family is
binomialand the link function islogit
Call:
glm(formula = Status ~ Age, family = binomial(link = "logit"),
data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4Logistic Regression in R
- we can fit a logistic regression model in R using the
glm()function glm()is a general function for fitting generalized linear models- for logistic regression, the family is
binomialand the link function islogit logitis the default so we can leave it out if we want:
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4Logistic Regression in R
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4- the model is: log\left(\frac{p}{1-p}\right) = 2.07 - 0.07(\mathrm{Age})
- or, equivalently: p = \frac{e^{2.07 - 0.07(\mathrm{Age})}}{1 + e^{2.07 - 0.07(\mathrm{Age})}}
Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
ggplot(aes(x=Age, y=prob)) +
geom_jitter(height=0.05, width=0) +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="glm", method.args=list(family="binomial"), se=FALSE, fullrange=TRUE, color="blue") +
lims(x=c(5,70), y=c(-0.05,1.05)) +
labs(title="Donner party (Males & Females)", y="Probability of Survival") +
theme_bw()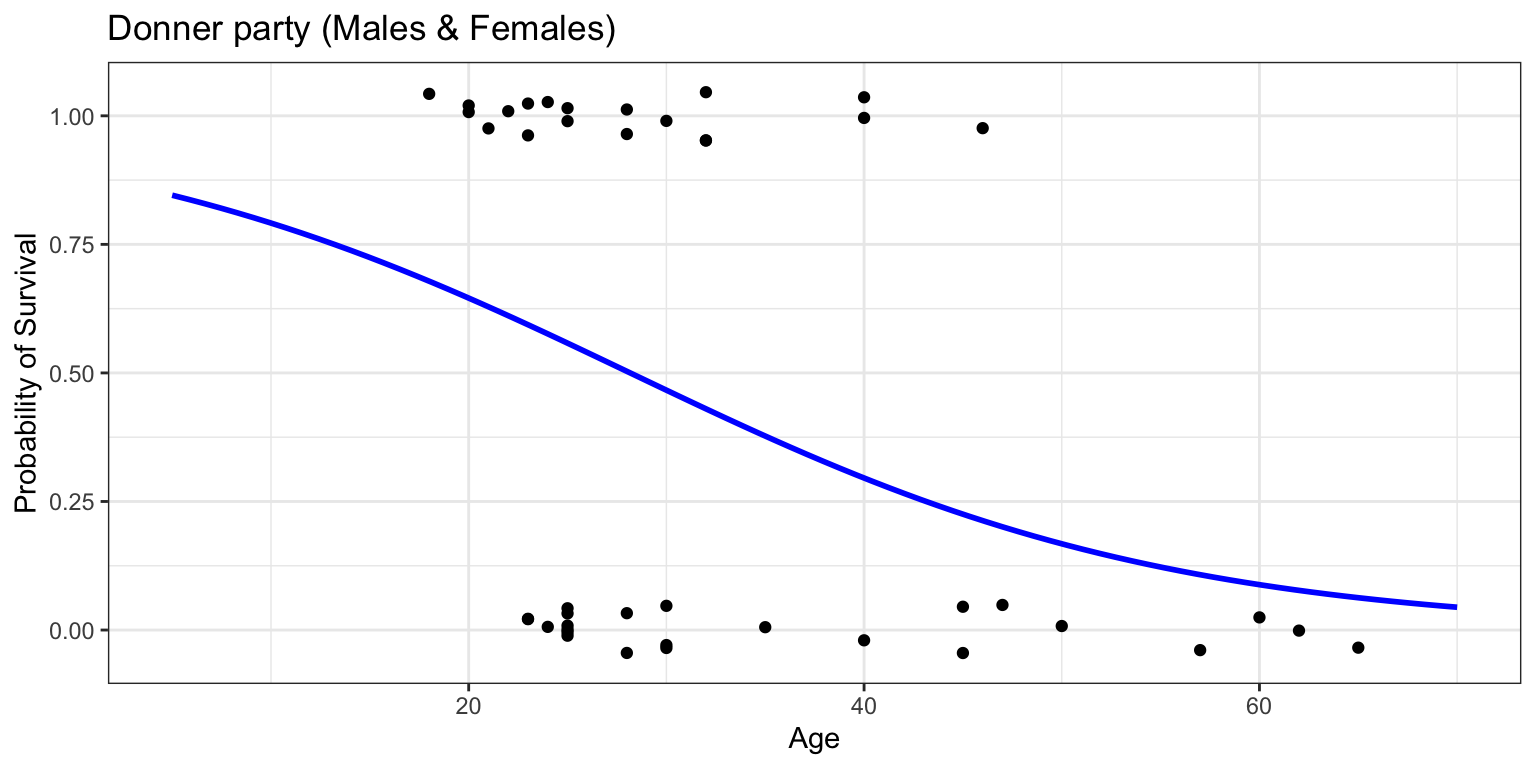
Prediction with Logistic Regression
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4- what is the probability of survival for a 40-year-old?
1
0.2956287 Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
ggplot(aes(x=Age, y=prob)) +
geom_jitter(height=0.05, width=0) +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="glm", method.args=list(family="binomial"), se=FALSE, fullrange=TRUE, color="blue") +
lims(x=c(5,70), y=c(-0.05,1.05)) +
geom_vline(xintercept=40, color="red") +
geom_hline(yintercept=prob_40, color="red") +
labs(title="Donner party (Males & Females)", y="Probability of Survival") +
theme_bw()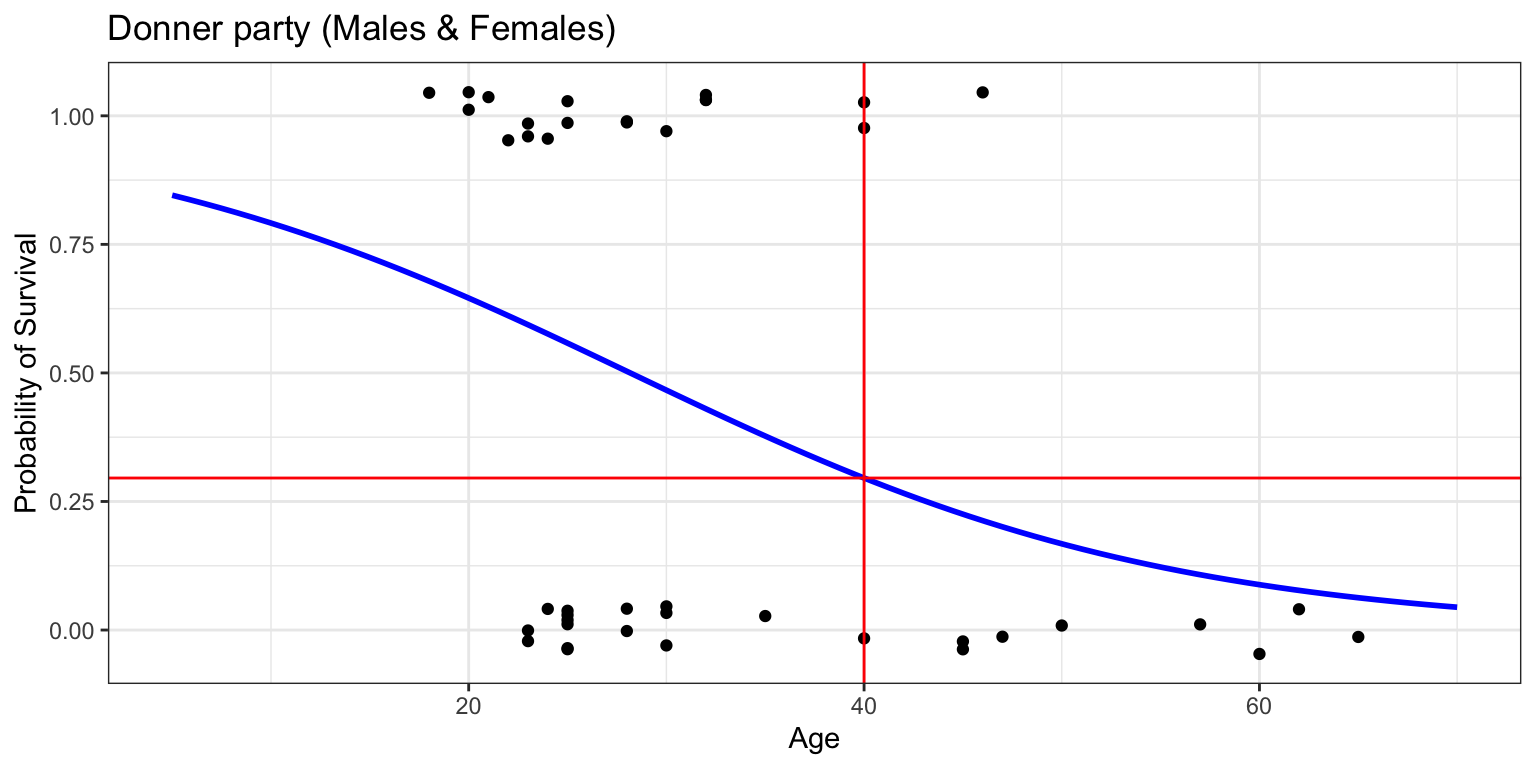
Interpretation of Logistic Regression Coefficients
- the regression coefficient of a variable corresponds to the change in log odds and its exponentiated form corresponds to the odds ratio
- the coefficients of a logistic regression model are in units of log odds
- the interpretation for a coefficient (a slope) is the change in log odds per unit change in the predictor variable
\begin{matrix} log\left(\frac{p}{1-p}\right) &= &2.07 - 0.07(\mathrm{Age})\\ p &= &\frac{e^{2.07 - 0.07(\mathrm{Age})}}{1 + e^{2.07 - 0.07(\mathrm{Age})}} \end{matrix}
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4Interpretation of Logistic Regression Coefficients
- e.g. the coefficient for Age is -0.07
- this means that for each additional year of age, the log odds of survival decreases by 0.07
- or, equivalently, the odds ratio of survival for (age+1) vs (age) is 0.93
- +1 unit of Age = 0.93 odds ratio of survival
- odds ratio > 1 : increase in odds of survival
- odds ratio < 1 : decrease in odds of survival
- not the same as 0.93 decrease in probability of survival (next slide)
\begin{matrix} log\left(\frac{p}{1-p}\right) &= &2.07 - 0.07(\mathrm{Age})\\ p &= &\frac{e^{2.07 - 0.07(\mathrm{Age})}}{1 + e^{2.07 - 0.07(\mathrm{Age})}} \end{matrix}
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4Odds vs Probability of outcome
- the odds of an outcome is the ratio of the probability of the outcome to the probability of the opposite outcome
- odds : \frac{p}{1-p}
- e.g. if the probability of survival is 0.8, then the odds of survival are 0.8/0.2 = 4
- the log odds of an outcome is the natural logarithm of the odds
- e.g. if the probability of survival is 0.8, then the log odds of survival are log(4) = 1.39
- the odds ratio is the ratio of odds between two situations
- the coefficients (slopes) of a logistic regression model are the change in the log odds per unit change in a continuous variable (e.g. Age) or a change in log odds across categories (e.g. Sex)
Interpretation of Logistic Regression Coefficients
- the coefficient for Age is -0.07
- this means that for each additional year of age, the log odds of survival decreases by 0.07
- or, equivalently, the odds ratio of survival is e^{-0.07} = 0.93 for an additional year of age
- +1 unit of Age = 0.93 odds ratio of survival
- An odds ratio > 1 implies a positive association between the predictor and the outcome
- An odds ratio < 1 implies a negative association between the predictor and the outcome
\begin{matrix} log\left(\frac{p}{1-p}\right) &= &2.07 - 0.07(\mathrm{Age})\\ p &= &\frac{e^{2.07 - 0.07(\mathrm{Age})}}{1 + e^{2.07 - 0.07(\mathrm{Age})}} \end{matrix}
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4Interpretation of Logistic Regression Coefficients
for example:
- Prob(Alive) for 40-year-old: p=0.296
- Prob(Alive) for a 41-year-old: p=0.281
- odds of survival for 40-year-old:
\mathrm{odds} = \frac{0.296}{1-0.296} = 0.42 - odds of survival for 41-year-old:
\mathrm{odds} = \frac{0.281}{1-0.281} = 0.39 - odds ratio of 41-yr old vs 40-yr old:
- \mathrm{odds\ ratio} = \frac{0.39}{0.42} = 0.93
- \log{(0.93)} = -0.07
\begin{matrix} log\left(\frac{p}{1-p}\right) &= &2.07 - 0.07(\mathrm{Age})\\ p &= &\frac{e^{2.07 - 0.07(\mathrm{Age})}}{1 + e^{2.07 - 0.07(\mathrm{Age})}} \end{matrix}
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4Logistic Regression with 2 Predictors
(Intercept) Age SexFemale
2.00466996 -0.08762745 1.50667376 Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
ggplot(aes(x=Age, y=prob, color=Sex)) +
geom_jitter(height=0.05, width=0) +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="glm", method.args=list(family="binomial"), se=FALSE, fullrange=TRUE) +
lims(x=c(5,70), y=c(-0.05,1.05)) +
labs(title="Donner party", y="Probability of Survival") +
theme_bw()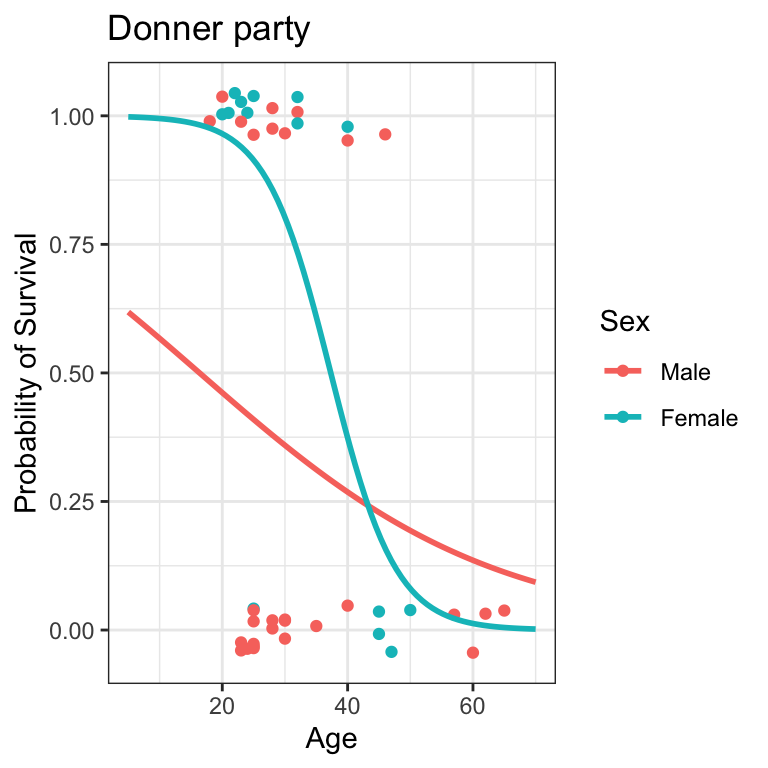
\begin{matrix} log\left(\frac{p}{1-p}\right) &= &2.0 - 0.09(\mathrm{Age}) + 1.5(\mathrm{SexFemale})\\ p &= &\frac{e^{2.0 - 0.09(\mathrm{Age}) + 1.5(\mathrm{SexFemale})}}{1 + e^{2.0 - 0.09(\mathrm{Age}) + 1.5(\mathrm{SexFemale})}} \end{matrix}
Interpretation of Logistic Regression Coefficients
\begin{matrix} log\left(\frac{p}{1-p}\right) &= &2.0 - 0.09(\mathrm{Age}) + 1.5(\mathrm{SexFemale})\\ p &= &\frac{e^{2.0 - 0.09(\mathrm{Age}) + 1.5(\mathrm{SexFemale})}}{1 + e^{2.0 - 0.09(\mathrm{Age}) + 1.5(\mathrm{SexFemale})}} \end{matrix}
- the coefficient for SexFemale is 1.5
- this means R coded Males as 0 and Females as +1
- the model for Males is:
log\left(\frac{p}{1-p}\right) = 2.0 - 0.09(\mathrm{Age}) + 1.5 (0) - the model for Females is:
log\left(\frac{p}{1-p}\right) = 2.0 - 0.09(\mathrm{Age}) + 1.5 (1)
Call:
glm(formula = Status ~ Age + Sex, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.00467 1.21857 1.645 0.1000 .
Age -0.08763 0.04084 -2.146 0.0319 *
SexFemale 1.50667 0.78497 1.919 0.0549 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 48.992 on 40 degrees of freedom
AIC: 54.992
Number of Fisher Scoring iterations: 5Interpretation of Logistic Regression Coefficients
- the coefficient for Age is -0.09
- this means that for each additional year of age, the log odds of survival decreases by 0.09
- or, equivalently, the odds ratio of survival is e^{-0.09} = 0.91 for an extra year of age
- +1 unit of Age = 0.91 odds ratio of survival
Call:
glm(formula = Status ~ Age + Sex, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.00467 1.21857 1.645 0.1000 .
Age -0.08763 0.04084 -2.146 0.0319 *
SexFemale 1.50667 0.78497 1.919 0.0549 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 48.992 on 40 degrees of freedom
AIC: 54.992
Number of Fisher Scoring iterations: 5Interpretation of Logistic Regression Coefficients
- the coefficient for SexFemale is 1.5
- this means that for Females the log odds of survival increases by 1.5 over Males
- or, equivalently, the odds ratio of survival for females vs males is e^{1.5} = 4.5
- odds = \frac{p}{1-p}
- log odds = \log(\frac{p}{1-p})
- \log(\frac{f}{1-f}) = \log(\frac{m}{1-m}) + 1.5
- \log(\frac{f}{1-f}) - \log(\frac{m}{1-m}) = 1.5
- \log(\frac{f}{1-f} / \frac{m}{1-m}) = 1.5
- \frac{f}{1-f} / \frac{m}{1-m} = e^{1.5} = 4.5
- \frac{\mathrm{odds\ female}}{\mathrm{odds\ male}} = e^{1.5} = 4.5
Call:
glm(formula = Status ~ Age + Sex, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.00467 1.21857 1.645 0.1000 .
Age -0.08763 0.04084 -2.146 0.0319 *
SexFemale 1.50667 0.78497 1.919 0.0549 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 48.992 on 40 degrees of freedom
AIC: 54.992
Number of Fisher Scoring iterations: 5Model Fit and Model Selection
- does adding Sex to the model improve the fit? Use AIC to compare models
Call:
glm(formula = Status ~ Age, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.06749 1.09914 1.881 0.0600 .
Age -0.07339 0.03510 -2.091 0.0366 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 53.134 on 41 degrees of freedom
AIC: 57.134
Number of Fisher Scoring iterations: 4
Call:
glm(formula = Status ~ Age + Sex, family = binomial, data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.00467 1.21857 1.645 0.1000 .
Age -0.08763 0.04084 -2.146 0.0319 *
SexFemale 1.50667 0.78497 1.919 0.0549 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 48.992 on 40 degrees of freedom
AIC: 54.992
Number of Fisher Scoring iterations: 5- AIC goes down when Sex is added to the model, so keep it in the model
- as in multiple regression we can use the
step()function to do stepwise model selection
Assumptions of Logistic Regression
- logistic regression does not require linearity (obviously)
- it does require that the predictors are linearly related to the log odds of the outcome
- we will test for this
- nor does it require normality of residuals
- but it does require that the residuals are independent
- there is no test of this, it’s conceptual
- nor does it require homoscedasticity
- it does require (obviously) that the dependent variable is binary
- we ought to know this by the nature of the variable
- like multiple regression, it does require that the predictors are independent of each other
- collinearity is a problem for logistic regression as it is for multiple regression
- we can test for this
Assumptions of Logistic Regression
- logistic regression typically requires a relatively large sample size to provide a stable model fit
- a rough minimum: 10 cases considering the least frequent outcome, for each predictor variable
- e.g. if we have 3 predictor variables, and the probability of the least frequent outcome is 0.3, the minimum sample size should be around (10 x 3)/0.3 = 100
- as with multiple regression, logistic regression is sensitive to outliers
- there are ways to test this
Check for log-odds linearity
- are the predictors linearly related to the log odds of the outcome?
cut()the predictorAgeinto bins usingquantile()- within each bin, compute log odds of
Survived
Code
donner %>%
mutate(prob = ifelse(Status == "Survived", 1, 0)) %>%
ggplot(aes(x=Age, y=prob)) +
geom_jitter(height=0.05, width=0) +
scale_y_continuous(breaks=seq(0,1,0.1)) +
geom_smooth(method="glm", method.args=list(family="binomial"), se=FALSE, fullrange=TRUE, color="blue") +
geom_vline(xintercept=quantile(donner$Age), color="red", lty=2) +
lims(x=c(5,70), y=c(-0.05,1.05)) +
labs(title="Donner party", y="Probability of Survival") +
theme_bw()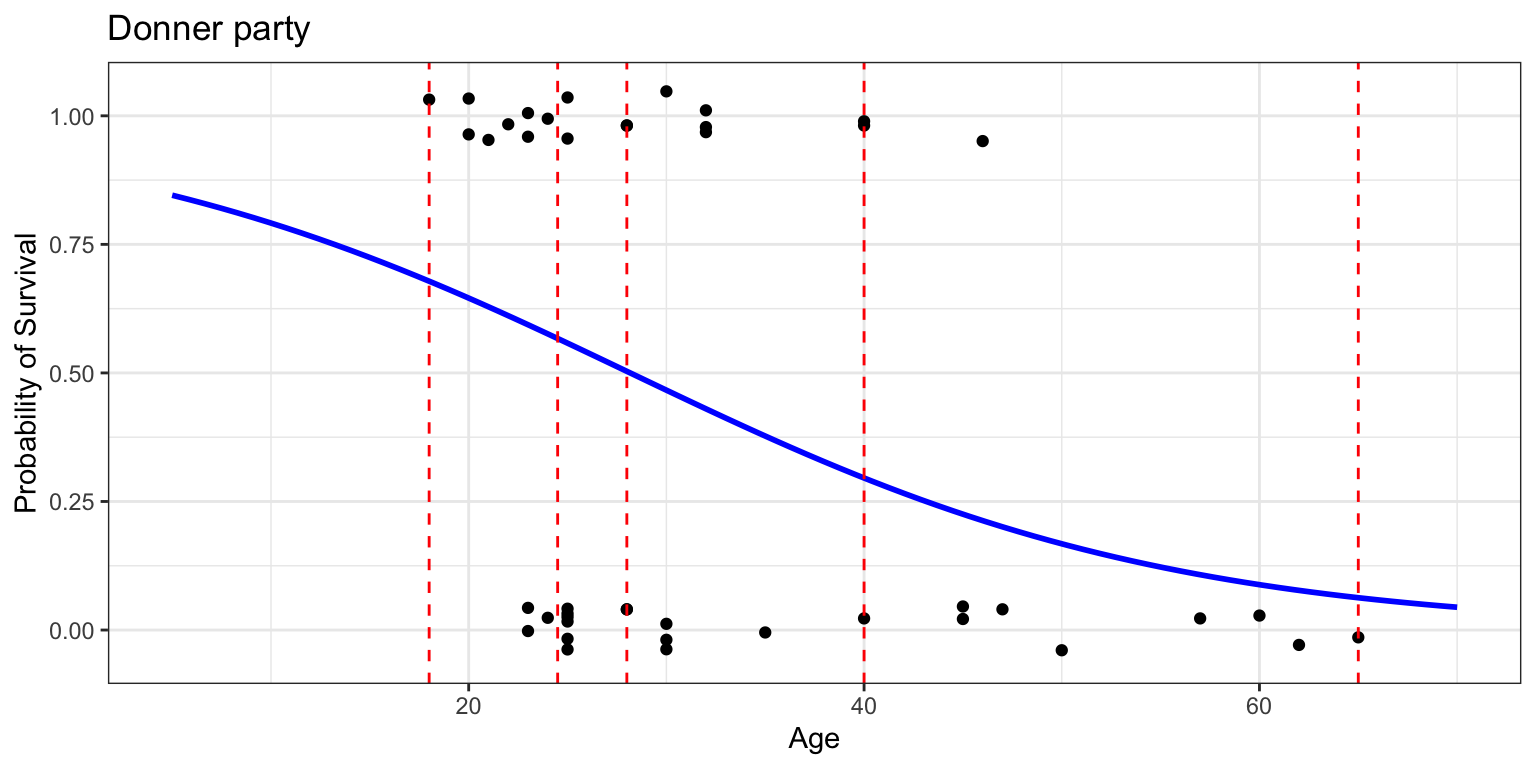
Check for log-odds linearity
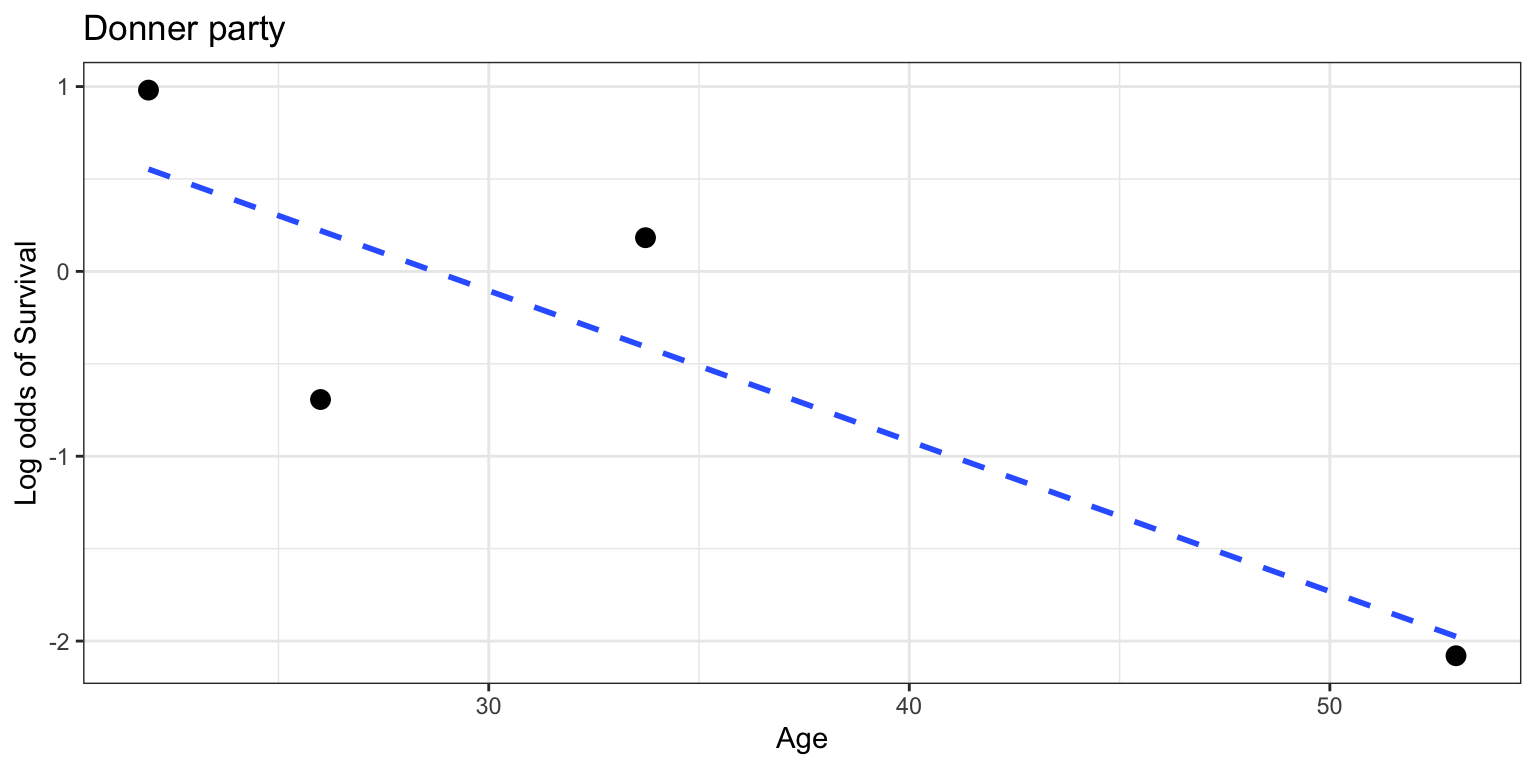
- then plot age vs log odds of survival within each quantile bin
- is it linear? sort of. maybe not.
- (second bin should be higher)
- but we don’t have much data in this toy dataset so 🤷
- you will see an example in the homework this week of a larger dataset
Box-Tidwell Test
- are the predictors linearly related to the log odds of the outcome?
- statistical test: Box-Tidwell test
- we test for the significance of the interaction between the predictor and the log odds of the outcome
- if there is an interaction between X and Y it means that
- the relationship between X and Y is different at different values of X
- i.e. the slope of the line relating X and Y is different at different values of X
- i.e. it’s not a constant slope, i.e. not a straight line, i.e. not linear, i.e. nonlinear
- if the Box-Tidwell test is significant, then the relationship between the predictor and the log odds of the outcome is nonlinear
Box-Tidwell Test
- we test for the significance of the interaction between the predictor and the log odds of the outcome
- in an R model formula, the notation
X:Ymeans “the interaction between X and Y” - so we simply add a term
Age:log(Age)to the GLM model Age:log(Age)means “the interaction between Age and log(Age)”- here:
p=0.7712so we are>.05so we fail to reject the null hypothesis that there is no interaction between Age and log odds of survival - the linearity assumption passes the Box-Tidwell test
Call:
glm(formula = Status ~ Age + Sex + (Age:log(Age)), family = binomial,
data = donner)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.60391 8.97625 -0.067 0.9464
Age 0.27300 1.23769 0.221 0.8254
SexFemale 1.52563 0.79610 1.916 0.0553 .
Age:log(Age) -0.07959 0.27374 -0.291 0.7712
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 59.028 on 42 degrees of freedom
Residual deviance: 48.902 on 39 degrees of freedom
AIC: 56.902
Number of Fisher Scoring iterations: 5Outliers
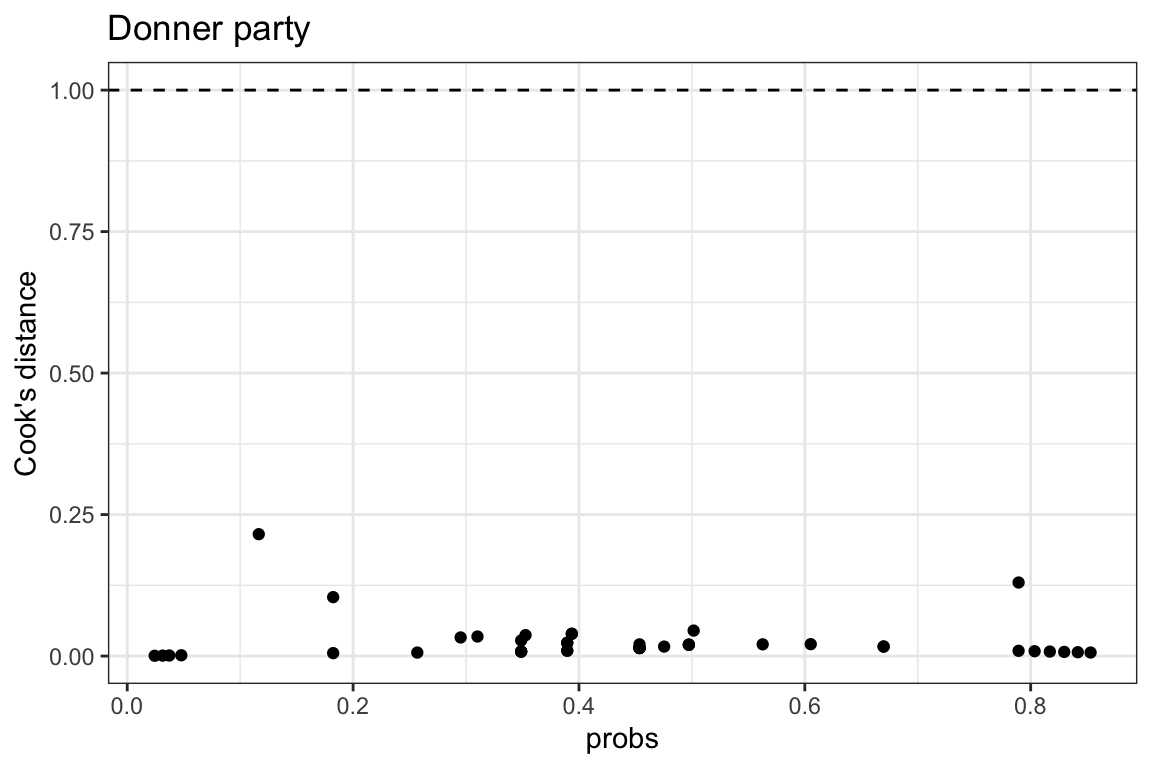
- use Cook’s distance
- Cook’s distance is a measure of the influence of each observation on the model
- observations with high Cook’s distance are outliers
- values > 1 are considered high
- all our values are < 1 so we’re ok
Collinearity
- as in multiple regression
- visualize using
ggpairs()from theGGallypackage - test using variance inflation factor (VIF)
- VIF ~ 4 or 5 is considered moderatly high and may be a problem
- VIF > 10 is considered high and is definitely a problem
- See Navarro 15.9.6 for more details
- she discusses it in the context of multiple regression
- the same principles apply to multiple continuous predictor variables in logistic regression