library(tidyverse)
x <- c(1,4,3,6,5,7,8)
y <- c(2,5,1,8,6,8,9)
n = 7
(b <- ((sum(y)*sum(x^2)) - (sum(x)*sum(x*y))) / ((n*sum(x^2)) - (sum(x))^2))[1] -0.2213115[1] 1.192623Week 3
? and m key during slidesThe regression line minimizes the sum of the (squared) residuals
regression minimizes the sum of the (squared) residuals
y = mx +b
y = \text{slope}*x + \text{yintercept}
We will also use this form:
y = \beta_{0} + \beta_{1}x
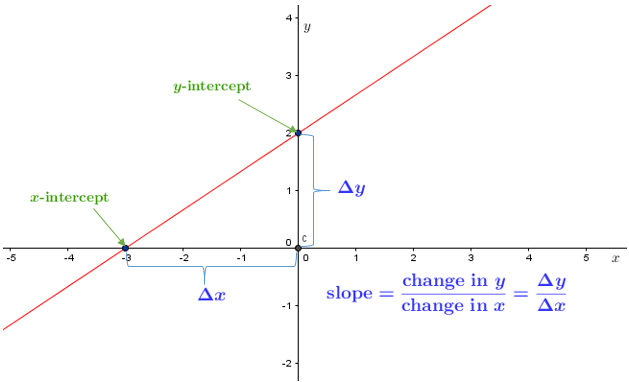
y = .5x + 2
What is the value of y, when x is 0?
y = .5*0 + 2
y = 0+2
y = 2
find m and b for:
Y = mX + b
so that the regression line minimizes the sum of the squared residuals
Y = mX + b
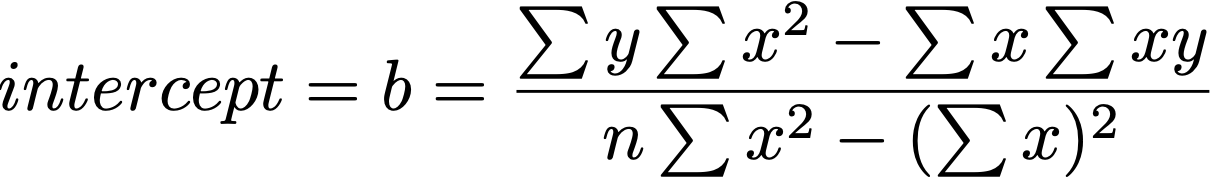

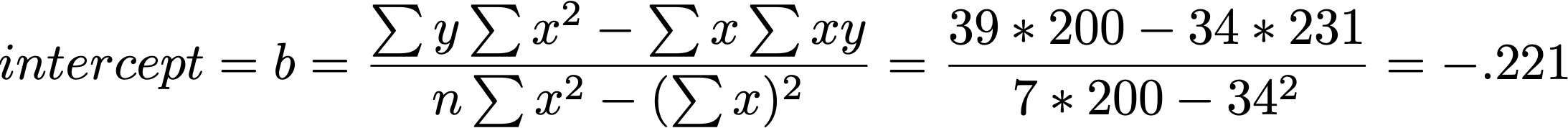
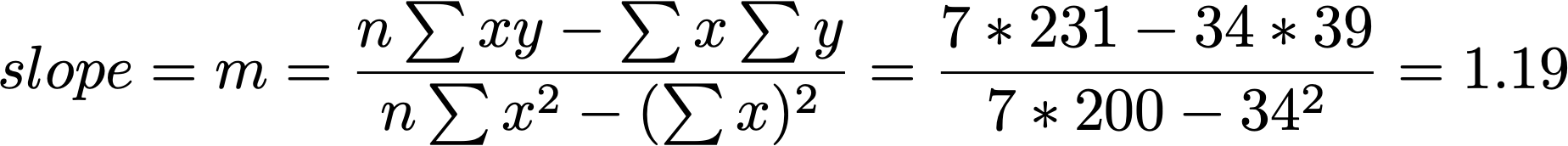
b = -0.221
m = 1.19
Y = (1.19)X - 0.221

lm()lm()What does the y-intercept mean?
It is the value where the line crosses the y-axis when x = 0
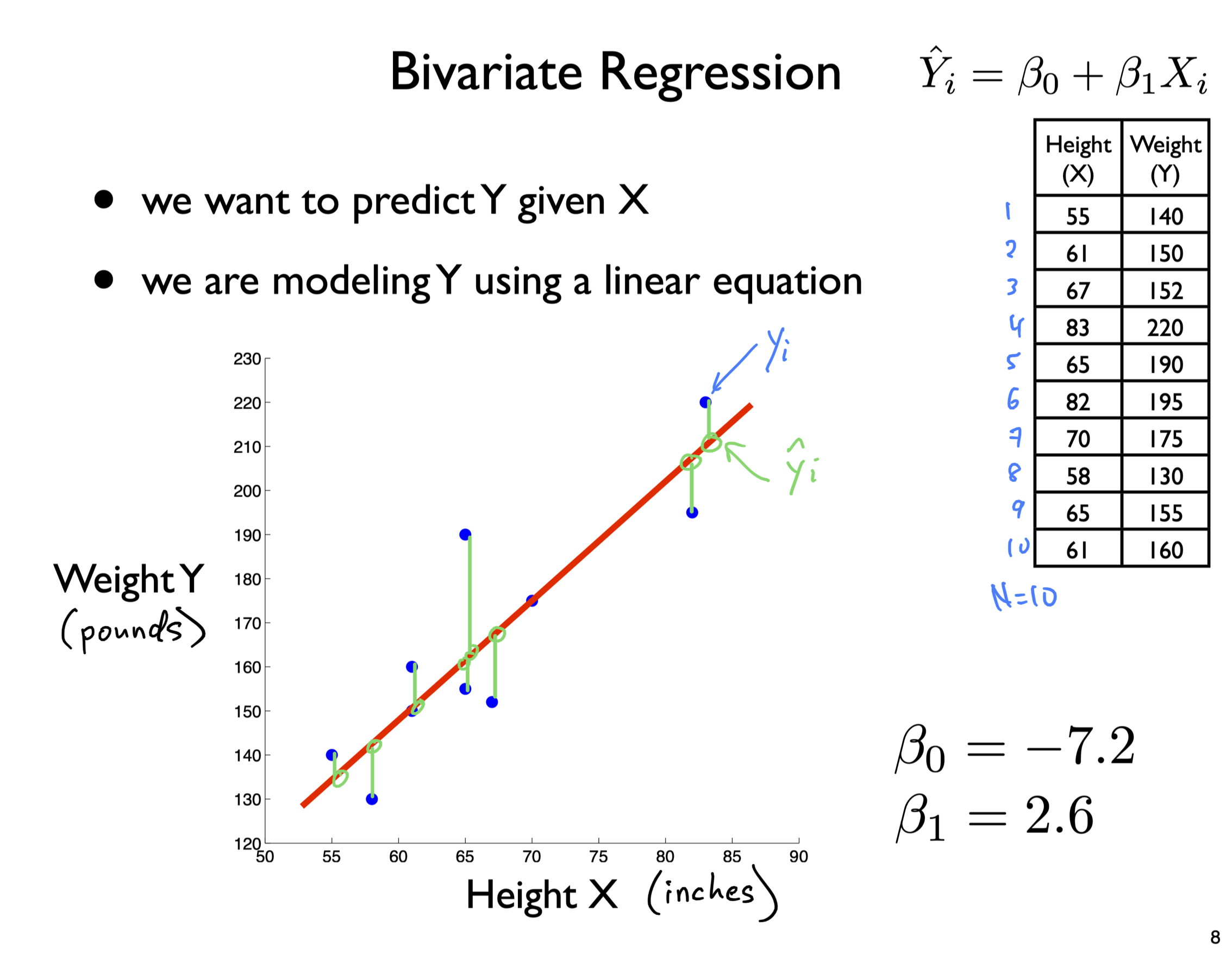
What does the slope mean?
The slope tells you the rate of change.
For every 1 unit of X, Y changes by “slope” amount
E.g., slope = 2.6
then for every 1 unit of X
Y increases by 2.6 units

Y_{i} = \hat{Y_{i}} + \varepsilon_{i}
\hat{Y}_{i} = \beta_{0} + \beta_{1} X_{i}
Sum of squared residuals is SS_{res} :
Total variability in Y is SS_{tot} :
SS_{res} = \sum_{i}(Y_{i} - \hat{Y}_{i})^{2}
SS_{tot} = \sum_{i}(Y_{i} - \bar{Y})^{2}
Sum of squared residuals is SS_{res} :
Total variability in Y is SS_{tot} :
SS_{res} = \sum_{i}(Y_{i} - \hat{Y}_{i})^{2}
SS_{tot} = \sum_{i}(Y_{i} - \bar{Y})^{2}
Coefficient of determination R^{2} :
R^{2} = 1 - \frac{SS_{res}}{SS_{tot}}
R^{2} is the proportion of variance in the outcome variable Y that can be accounted for by the predictor variable X
R^{2} always falls between 0.0 and 1.0
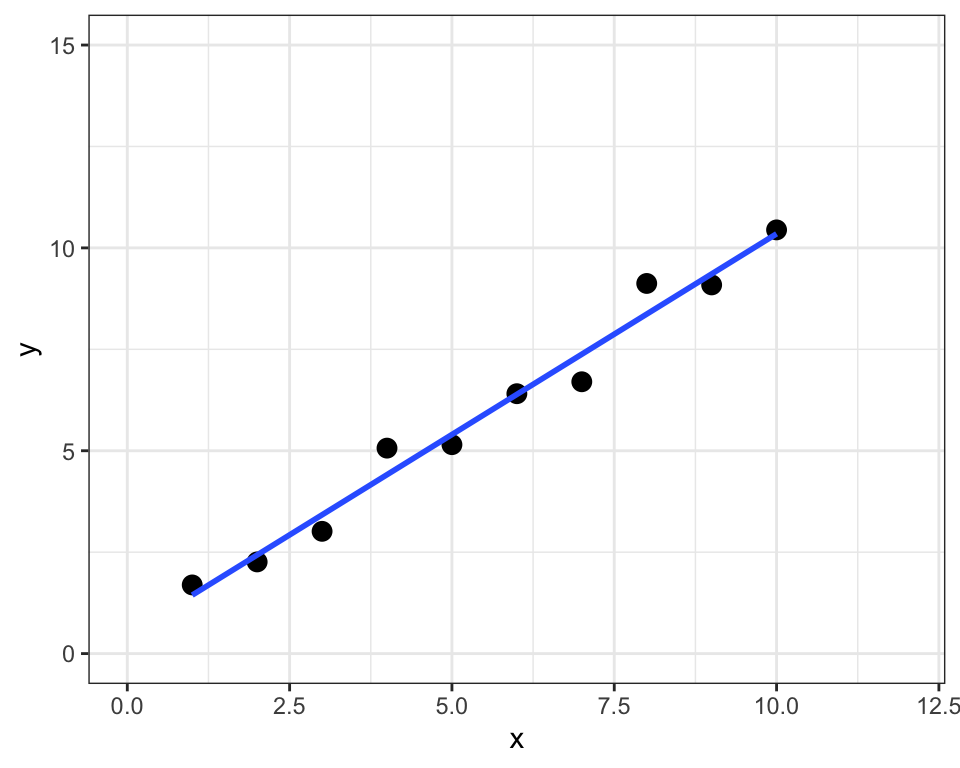
sum of squared residuals = 1.9sum of squared total = 82.6R-squared = 0.98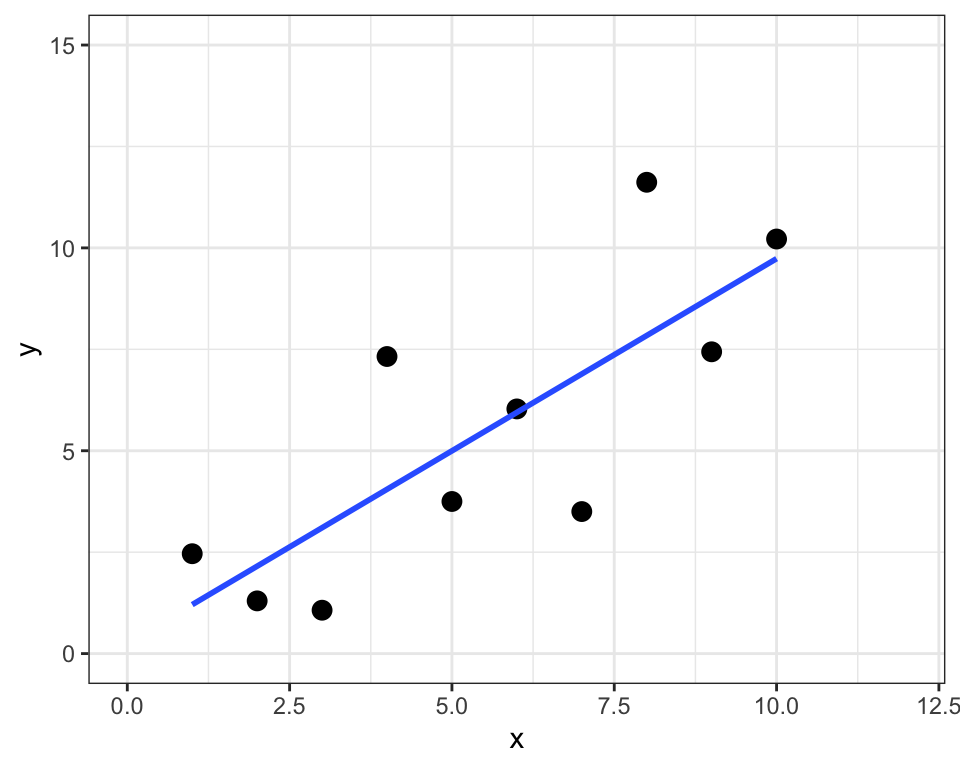
sum of squared residuals = 46.5sum of squared total = 120.6R-squared = 0.61\sigma_{est} = \sqrt{\frac{\sum(Y-\hat{Y})^{2}}{N}}
\sigma_{est} = \sqrt{\frac{\sum(Y-\hat{Y})^{2}}{N}}
s_{est} = \sqrt{\frac{\sum_{i}(Y_{i}-\hat{Y}_{i})^{2}}{N-2}}

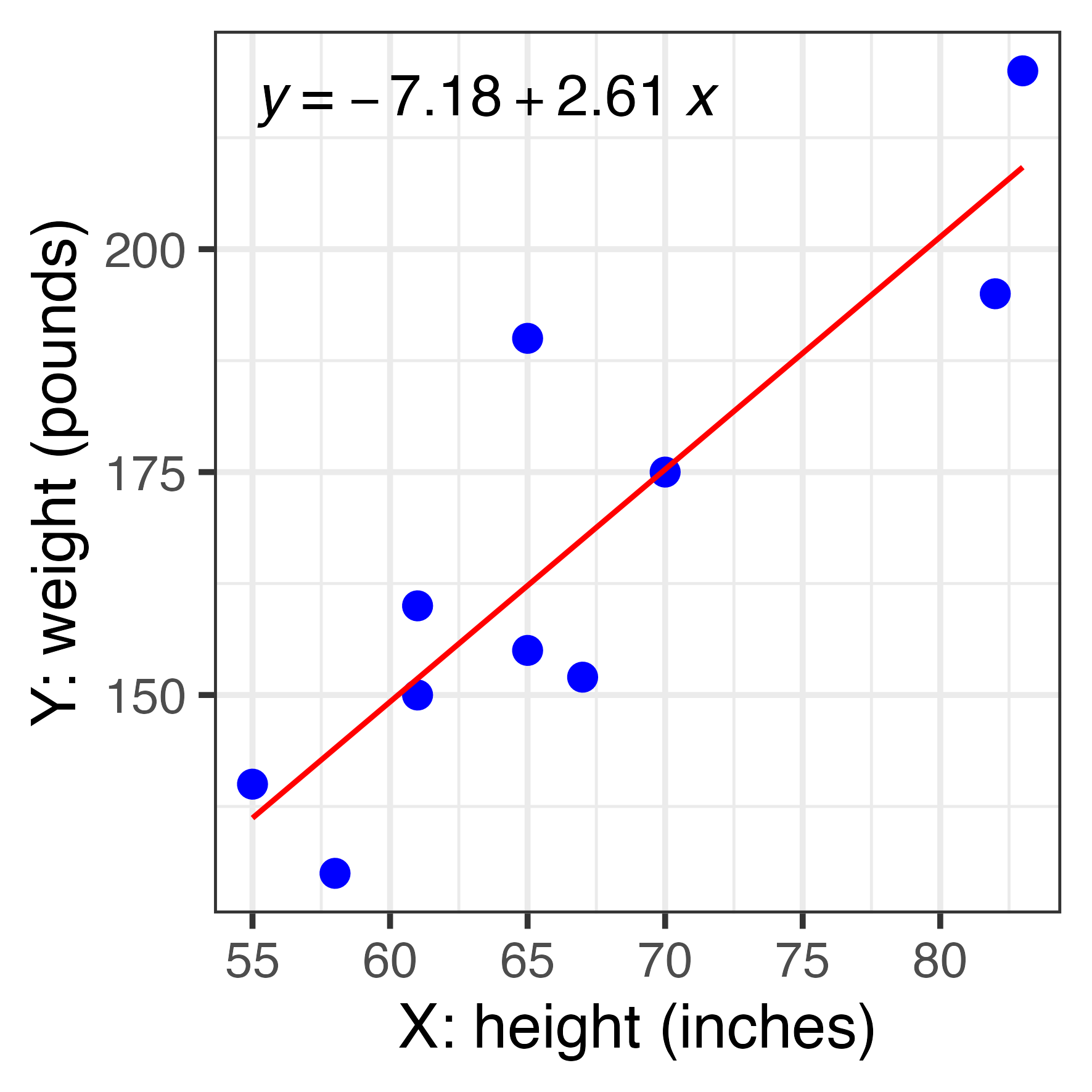
Y = -7.2 + 2.6 X
R^{2} = 0.772
s_{est} = 14.11 (pounds)

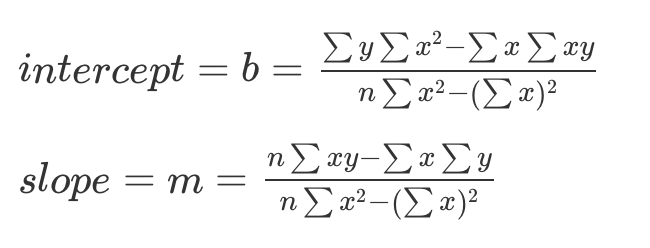
summary() of our lm() in R: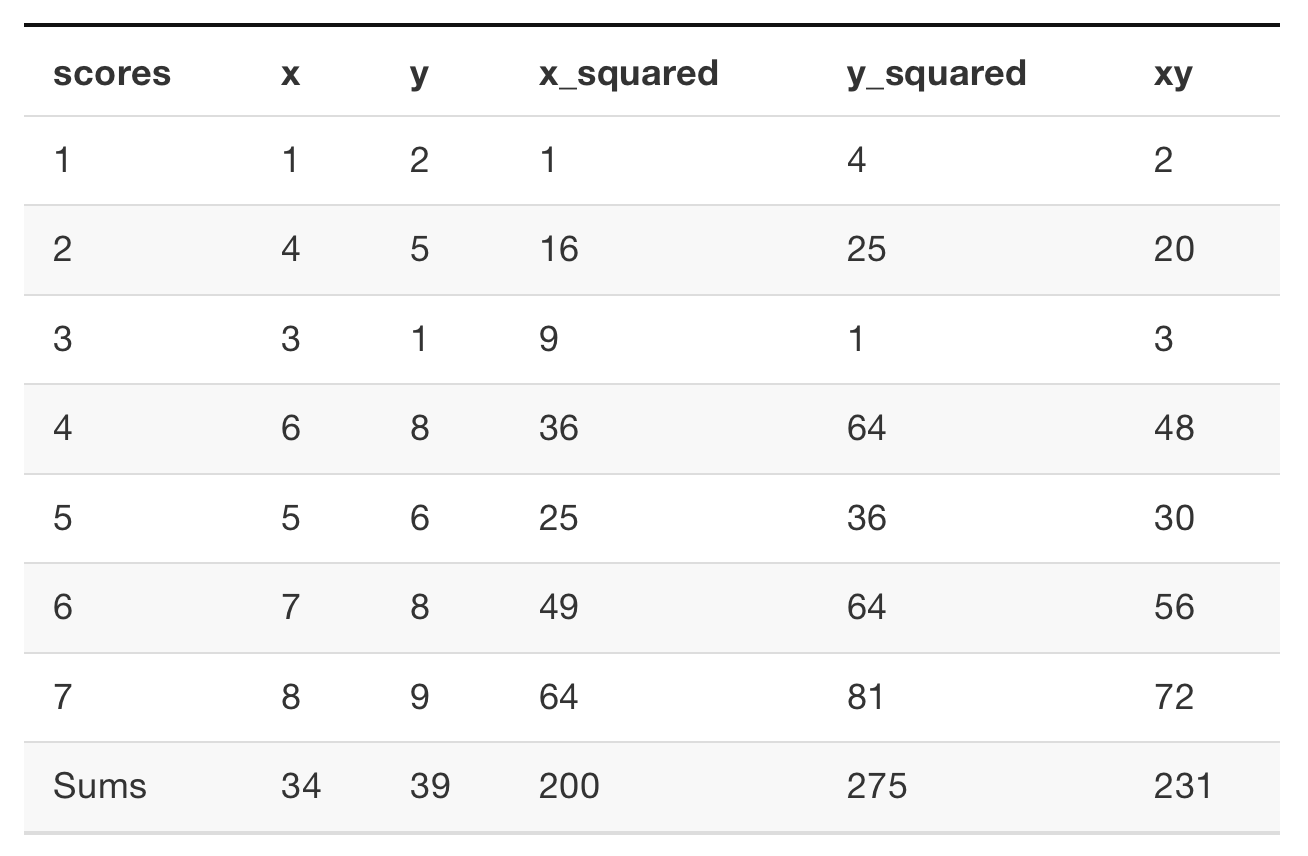
summary() of our lm() in R: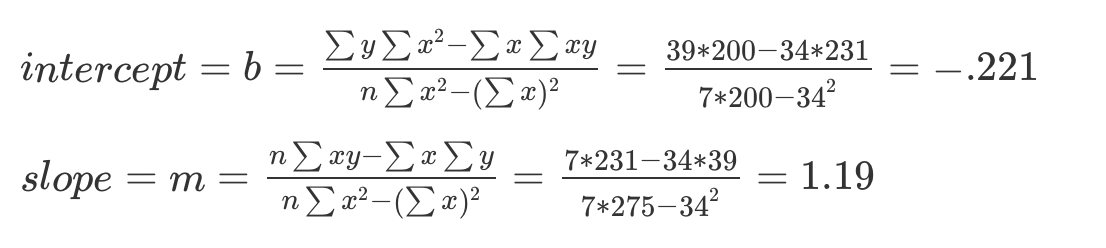
\bar{X} \pm t_{(0.975,N-1)} \left( \frac{s}{\sqrt{N}} \right)
\bar{X} \pm t_{(0.975,N-1)} \left( \frac{s}{\sqrt{N}} \right)
recall our regression model:
Y = -7.18 + 2.61 X
we can also compute 95% CIs for coefficients (\beta_{0},\beta_{1})
CI(b) = \hat{b} \pm \left( t_{crit} \times SE(\hat{b}) \right)
d <- tibble(x=c(55,61,67,83,65,82,70,58,65,61),
y=c(140,150,152,220,190,195,175,130,155,160))
mymod <- lm(y ~ x, data = d)
coef(mymod)(Intercept) x
-7.176930 2.606851 2.5 % 97.5 %
(Intercept) -84.898712 70.544852
x 1.451869 3.761832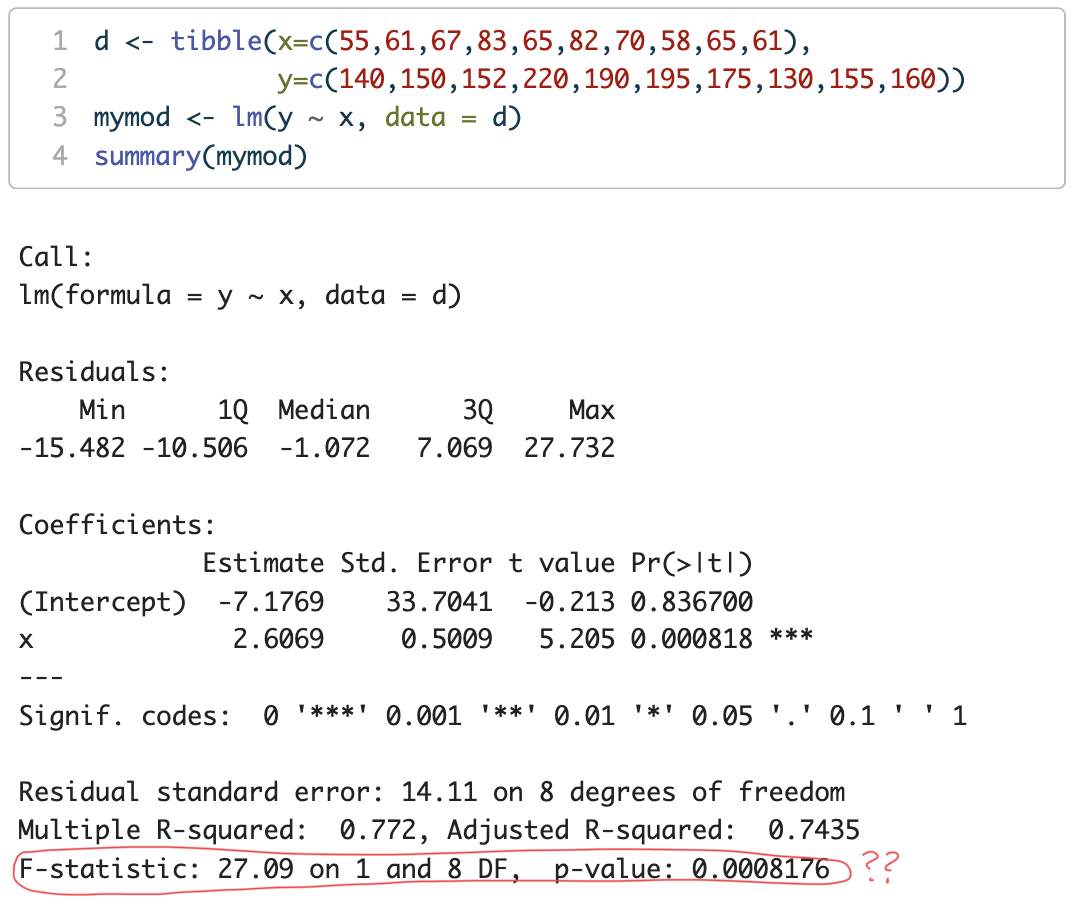
F(1,8)=27.09
p=0.0008176
→ what is this hypothesis test of?
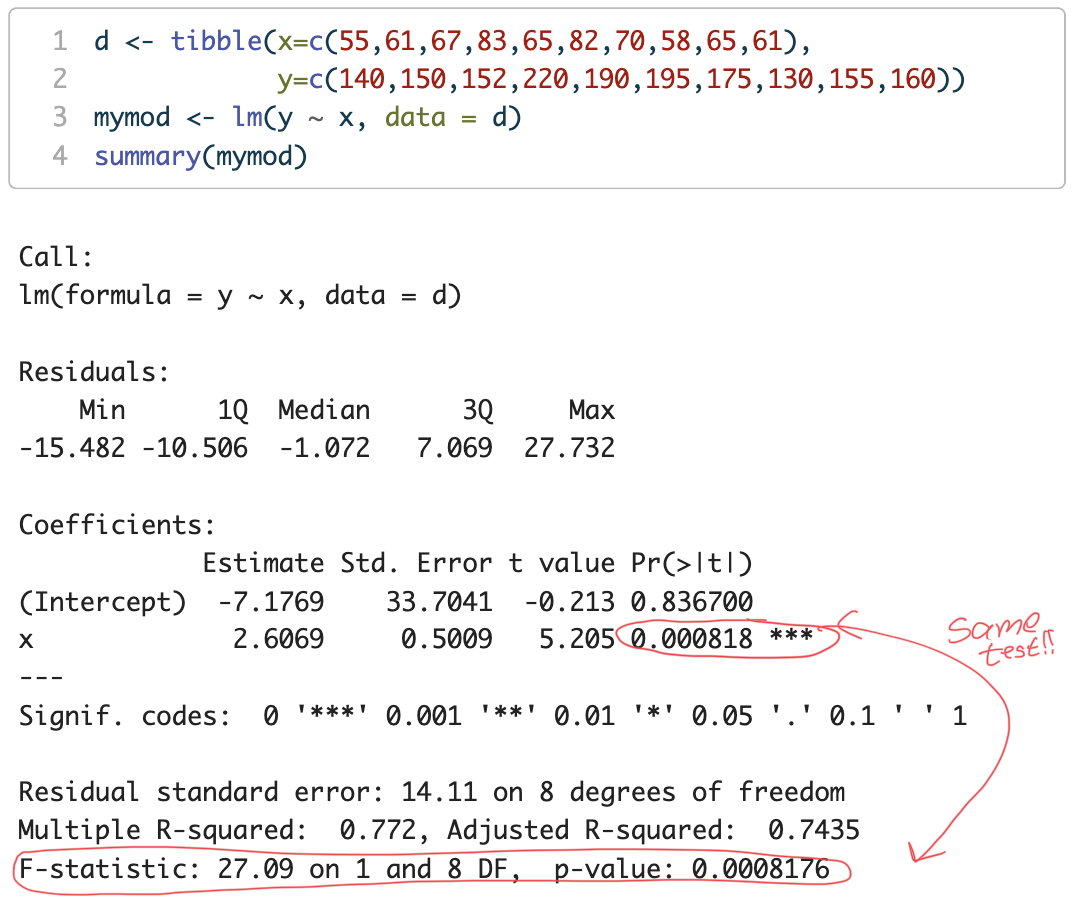
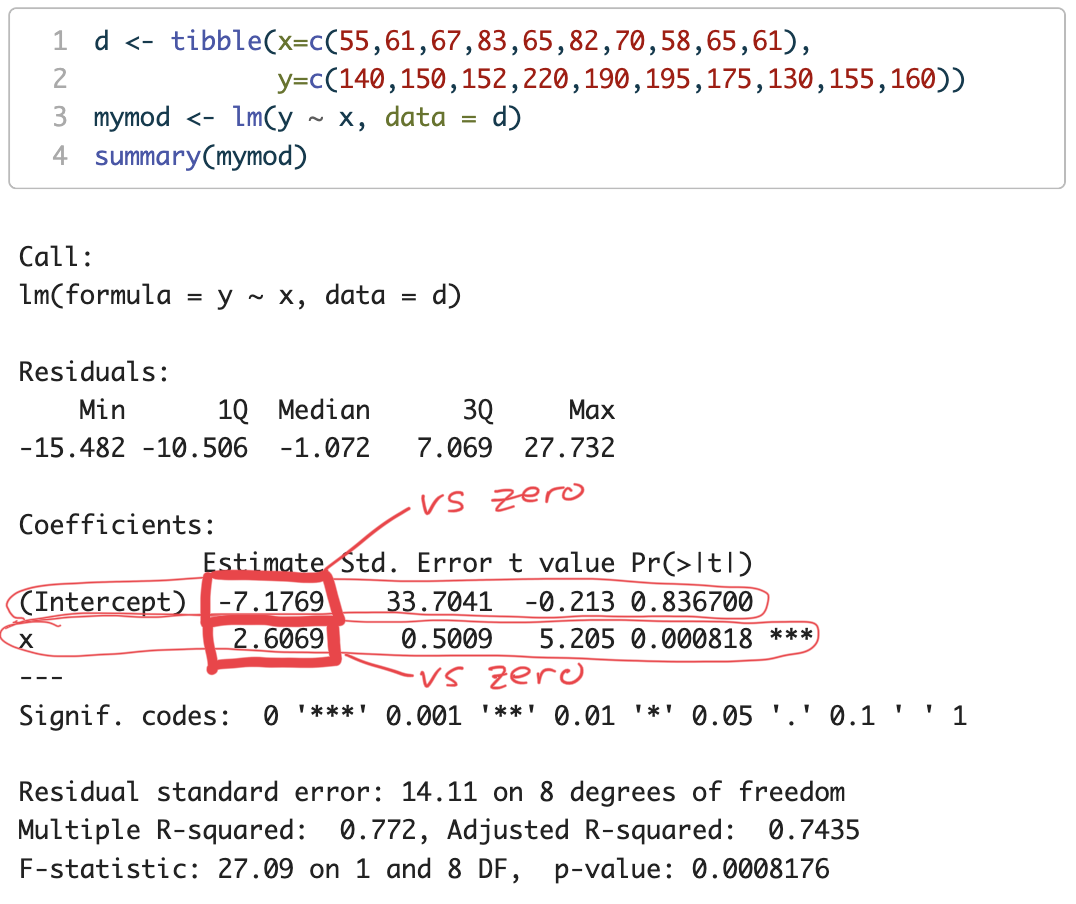
intercept (\beta_{0}) = -7.1769
p = 0.836700
Under the null hypothesis H_{0} the probability of obtaining an intercept as large (farthest from zero) as -7.1769 due to random sampling is 83.67%
That is pretty high! We cannot really reject H_{0}
We cannot reject H_{0} (that the intercept = zero)
We infer that the intercept is most likely = zero
slope (\beta_{1}) = 2.6069
p = 0.000818
Under the null hypothesis H_{0} the probability of obtaining a slope as large (farthest from zero) as 2.6069 due to random sampling is 0.0818%
That is pretty low! We will reject H_{0} that the slope is zero
The slope is not zero. What is it?
Our estimate of the slope is \beta_{1} = 2.6069
Our 95% confidence interval is [1.451869, 3.761832] from confint()
shapiro.test() (Shapiro-Wilk test)shapiro.test(residuals(my.mod))bptest() (Breusch-Pagan test)car package: ncvTest() (non-constant variance test)ncvTest() to the lm() model object: ncvTest(my.mod)